I. Контрольная работа №5

Кафедра физики

 

КОНТРОЛЬНЫЕ ЗАДАНИЯ

ПО ФИЗИКЕ

 

ДЛЯ СТУДЕНТОВ ЗАОЧНИКОВ

ИНЖЕНЕРНО-ТЕХНИЧЕСКИХ СПЕЦИАЛЬНОСТЕЙ

 

 

Часть III

 

Волновая оптика,

Квантовая оптика

 

В В Е Д Е Н И Е

 

Целью настоящего учебного издания является оказание помощи студентам заочникам инженерно-технических специальностей высших учебных заведений в изучении физики.

Настоящее учебное издание является третей частью, состоящего из четырёх частей, учебного издания, охватывающего весь курс физики. Для удобства обучающихся каждая из частей издаётся отдельным изданием.

Каждая часть содержит две таблицы с номерами задач. Задачи располагаются сразу после таблиц. Номера задач, которые должен решить студент, расположены в строке, соответствующей последней цифре номера его зачётной книжки. Числа, соответствующие последней цифре номера зачётной книжки, расположены в крайнем левом столбце каждой из таблиц.

Столбцы таблицы нумерованы и соответствуют определённой теме курса физики. Название темы и номер её столбца совпадает с номером и названием подпункта Содержания.

 

С О Д Е Р Ж А Н И Е

Стр.

I. Контрольная работа № 5. Волновая оптика. ………………………….4

5.1. Геометрическая оптика - построения в линзах. (№№ 501 – 510)

5.2. Электромагнитная волна (ее уравнение). (№№ 511 – 520)

5.3. Определение оптической длины пути и разности хода. (№№ 521 – 530)

5.4. Интерференция: кольца Ньютона, тонкая пленка и клин. (№№ 531 – 540)

5.5.1. Дифракция. Зоны Френеля на круглом отверстии. (№№ 541 – 550)

5.5.2. Дифракция на дифракционной решётке и на одиночной щели. (№№ 551 – 560)

5.6. Поляризация света. Законы Малюса и Брюстера. Вращение плоскости поляризации. (№№ 561 – 570)

 

II. Контрольная работа № 6. Квантовая оптика. ……………………..12

6.1. Абсолютно чёрное тело. Законы Стефана-Больцмана и Вина. (№№ 601 – 610)

6.2. Фотон и его свойства. (№№ 611 – 620)

6.3. Фотоэффект (малые скорости фотоэлектронов). (№№ 621 – 630)

6.4. Фотоэффект (релятивистские скорости фотоэлектронов). (№№ 631 – 640)

6.5. Эффект Комптона. (№№ 641 – 650)

6.6. Световое давление. (№№ 651 – 660)

6.7. Тормозное рентгеновское излучение. (№№ 661 – 670)

 

III. Справочные материалы.……………………………………………….22

3.1 Основные законы и формулы

3.2 Физические величины и их единицы в системе СИ

3.3 Таблицы констант

IV. Литература. ……………………………………………………………….31

I. Контрольная работа №5

 

Таблица № 5: номера задач по темам
Последняя цифра зачетной книжки	Номера тем
5.1	5.2	5.3	5.4	5.5.1	5.5.2	5.6
Номера задач

 

 

501. На расстоянии 15 см от двояковыпуклой стеклянной линзы, радиусы кривизны которой R₁ = R₂ = 50 см, поставлен перпендикулярно оптической оси предмет высотой h = 2 см. Найти положение и высоту изображения. Решение пояснить рисунком.

502. Двояковыпуклая стеклянная линза, ограниченная сферическими поверхностями одинакового радиуса кривизны R₁ = R₂ = 12 см, поставлена на такое расстояние от предмета, что изображение на экране получилось в k = 20 раз больше предмета. Определить расстояние от предмета до экрана. Решение пояснить рисунком.

503. Плосковыпуклая линза с радиусом кривизны R = 30 см и показателем преломления n = 1,5 дает изображение предмета с увеличением, равным k = 2. Найти расстояние предмета и изображения до линзы. Решение пояснить рисунком.

504. На расстоянии 40 см перед двояковыпуклой линзой с одинаковыми радиусами кривизны R₁ = R₂ = 8 см и показателем преломления n = 1,5 на оптической оси находится светящаяся точка. Найти положение изображения этой точки. Решение пояснить рисунком.

505. На расстоянии 50 см от двояковыпуклой стеклянной линзы, радиусы кривизны которой R₁ = R₂ = 30 см, поставлен перпендикулярно оптической оси предмет высотой h = 2 см. Найти положение и высоту изображения, если вся система помещена в сероуглерод. Решение пояснить рисунком.

506. Из двух стекол с показателями преломления n₁ = 1,5 и n₂ = 1,7 сделаны две одинаковые двояковыпуклые линзы. 1) Найти отношение их фокусных расстояний. 2) Какое действие каждая из этих линз произведет на луч, параллельный оптической оси, если линзы погрузить в прозрачную жидкость с показателем преломления n₃ = 1,6? Решение пояснить рисунком.

507. Лупа, представляющая собой двояковыпуклую линзу, изготовлена из стекла с показателем преломления n = 1,6. Радиусы кривизны поверхностей линзы одинаковы и равны R₁ = R₂ = 12 см. Определить увеличение лупы, если глаз расположен от лупы на расстоянии b = 25 см. Решение пояснить рисунком.

508. Тонкая линза, помещенная в воздухе, обладает оптической силой D₁ = 5 дптр, а в некоторой жидкости D₂ = – 0,48 дптр. Определить показатель преломления жидкости, если показатель преломления стекла, из которого изготовлена линза n = 1,52. Показать на рисунках, как будут преломляться лучи, падающие на линзу параллельно главной оптической оси в этих двух случаях.

509. На расстоянии 20 см перед двояковыпуклой линзой с одинаковыми радиусами кривизны R₁ = R₂ = 10 см и показателем преломления n = 1,5 на оптической оси находится предмет. Найти положение изображения этого предмета. Как изменится положение предмета, если всю систему поместить в сероуглерод? Решение пояснить рисунком.

510. На расстоянии 20 см перед двояковыпуклой линзой с одинаковыми радиусами кривизны R₁ = R₂ = 40 см и показателем преломления n = 1,5 на оптической оси находится предмет. Во сколько раз изображение будет больше самого предмета? Решение пояснить рисунком.

511. Напряженность электрического поля плоской электромагнитной волны имеет следующие компоненты: Е_х = 0; Е_у = 0; Е_z = 2 cos[π∙10¹⁵ (t – x/c)], (где с = 3∙10⁸ м/с). Волна распространяется вдоль оси Х. Записать компоненты для напряженности магнитного поля данной волны.

512. Электромагнитная волна распространяется вдоль оси У в отрицательном направлении. В некоторый момент времени и в некоторой координате напряженность электрического поля Е направлена вдоль оси Z и имеет величину 100 В/м. Найти величину и направление вектора напряженности магнитного поля Н в той же точке и в тот же момент времени.

513. Определить величину интенсивности радиоволны, если величина вектора напряженности электрического поля Е = 5 В/м. Какова величина вектора напряженности магнитного поля H этой волны? Волну считать плоской.

514. Найти связь интенсивности электромагнитной волны I с напряженностью электрического поля E.

515. Показать, что уравнение плоской волны Е_у=Е_осоs(ωt-kx+φ_о) является решением волнового уравнения.

516. Солнечный луч достиг поверхности Земли с интенсивностью I = 1,4 кВт/м2. Вычислить амплитудные значения для напряженностей электрического E и магнитного H полей, считая волну плоской.

517. Найти связь интенсивности электромагнитной волны I с напряженностью магнитного поля H.

518. Показать, что уравнение плоской волны H_z=H_о sin(ωt-kx+φ_о) является решением волнового уравнения.

519. Определить величину интенсивности I плоской электромагнитной волны, если величина вектора напряженности магнитного поля Н = 0,015 А/м. Какова величина вектора напряженности электрического поля E этой волны?

520. Найти величины напряженностей электрического E и магнитного H полей плоской электромагнитной волны на расстоянии пяти длин волн от источника через 10¾ периода после начала испускания волны, если амплитудное значение напряженности электрического поля Е₀ = 10 В/м и считать, что колебания происходят по закону синуса.

521. Сколько длин волн монохроматического света с частотой колебаний ν = 5·10¹⁴ Гц уложится на пути длиной l = 1,2 мм: I) в вакууме; 2) в стекле?

522. Определить длину l₁ отрезка, на котором укладывается столько же длин волн в вакууме, сколько их укладывается на отрезке l₂ = 3 мм в воде.

523. Какой путь l₁ пройдет фронт волны монохроматического света в вакууме за то же время, за которое он проходит путь длиной l₂ = 1 м в воде?

524. На пути световой волны, идущей в воздухе, поставили стеклянную пластинку толщиной d = 1 мм. На сколько изменится оптическая длина пути, если волна падает на пластинку 1) нормально; 2)под углом α = 30^о?

525. На пути монохроматического света с длиной волны λ = 0,6 мкм находится плоскопараллельная стеклянная пластина толщиной d = 0,1 мм. Свет падает на пластину нормально. На какой угол следует повернуть пластину, чтобы оптическая длина пути изменилась на λ/2, если показатель преломления пластины n = 1,5?

526. Два параллельных пучка световых волн I и II падают на тонкую призму с преломляющим углом α = 30⁰ на расстоянии d = 2 см и после преломления выходят из нее (рис. 5-1). Найти оптическую разность хода световых волн после преломления их призмой.

 

 

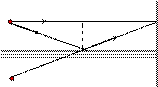
I S P

d a

II M

S’

 

Рис. 5 - 1 Рис. 5 - 2

 

527. На пути монохроматического света с длиной волны λ = 0,6 мкм находится плоскопараллельная стеклянная пластина толщиной d = 0,1 мм. Свет падает на пластину нормально. Как изменится оптическая длина пути, если стеклянную пластину заменить моноксидом силикона с показателем преломления n = 2,0?

528. Найти все длины волн видимого света (от λ = 0,76 мкм, до λ = 0,38 мкм), которые будут: 1) максимально усилены; 2) максимально ослаблены при оптической разности хода интерферирующих волн, равной Δ = 1,8 мкм.

529. Источник света с длиной волны λ = 0,6 мкм и плоское зеркало расположены, как показано на рисунке 5 - 2 (зеркало Ллойда). Что будет наблюдаться на экране в точке Р, где накладываются лучи SP и SMP, - свет или темнота (максимум или минимум), если SP = 2 м, a = 0,55 мм, SM = MP?

530. На пути монохроматического света с длиной волны λ = 0,6 мкм находится плоскопараллельная стеклянная пластина толщиной d = 0,1 мм. Свет падает на пластину нормально. На сколько следует увеличить толщину пластины, чтобы оптическая длина пути изменилась на λ/2, если показатель преломления пластины n = 1,5?

531. Материал линзы, в опыте с кольцами Ньютона, имеет показатель преломления n₁, а стеклянная пластинка – n₃, и зазор между ними заполнен веществом с показателем преломления n₂ = 1,55, при чем n₁>n₂>n₃. Найти радиус 8-го светлого кольца Ньютона в отраженном свете, если радиус кривизны линзы R = 3,1 м, а длина волны λ = 490 нм.

532. Между стеклянной пластинкой и лежащей на ней плосковыпуклой линзой находится жидкость. Найти показатель преломления жидкости, если радиус 3-го темного кольца Ньютона в отраженном свете с длиной волны λ = 0,6 мкм равен r₃ = 0,82 мм. Радиус кривизны линзы R = 0,5 м.

533. Для получения колец Ньютона используют плоско-выпуклую линзу с радиусом кривизны R = 12,5 м. Освещая линзу монохроматическим светом, определили, что расстояние между 4-м и 5-м светлыми кольцами в отраженном свете равно 0,5 мм. Найти длину волны падающего света.

534. Установка для наблюдения колец Ньютона освещается нормально падающим светом с длиной волны λ = 590 нм. Радиус кривизны линзы равен R = 5 см. Определить толщину воздушного зазора в том месте, где в отраженном свете наблюдается третье светлое кольцо.

535. На тонкий стеклянный клин, с показателем преломления стекла n = 1,52, нормально падает монохроматический свет. Наименьшая толщина клина, с которой видны интерференционные полосы d = 0,1 мкм, расстояние между полосами b = 5 мм. Определить длину волны падающего света и угол между поверхностями клина.

536. Какую наименьшую толщину должна иметь пленка из скипидара (показатель преломления скипидара n = 1,48), если на нее под углом 30⁰ падает белый свет, и она в проходящем свете кажется желтой? Длина волны желтых лучей λ = 0,58 мкм.

537. На тонкую пленку из глицерина с показателем преломления n = 1,47 падает белый свет под углом α₁ = 30⁰. В отраженном свете пленка кажется светло-зеленой (длина волны λ = 0,540 мкм). Каким будет казаться цвет пленки в отраженном свете, если свет будет падать под углом α₂ = 60⁰.

538. Между двумя плоскопараллельными пластинами на расстоянии b = 10 см от границы их соприкосновения находится проволока диаметром d = 0,01мм, образуя воздушный клин. Пластины освещаются нормально падающим монохроматическим светом (длина волны λ = 0,6 мкм). Определить ширину интерференционных полос, наблюдаемых в отраженном свете.

539. На тонкую глицериновую пленку толщиной d = 1,5 мкм и с показателем преломления n = 1,47 нормально падает белый свет. Определить длины волн лучей видимого участка спектра (0,4≤ λ ≤ 0,8 мкм), которые будут ослаблены в результате интерференции.

540. Расстояние между двумя когерентными источниками света d = 2 мм, они удалены от экрана на L = 2 м. Найти длину волны, излучаемую данными источниками, если расстояние на экране между 3-им и 5-ым минимумами интерференционной картины b = 1,2 см.

541. На диафрагму с круглым отверстием радиусом r = 1 мм падает нормально параллельный пучок света с длиной волны λ = 500 нм. На пути лучей, прошедших через отверстие, помещают экран. Определить максимальное расстояние от центра отверстия до экрана, при котором в центре дифракционной картины еще будет наблюдаться темное пятно.

542. Плоская световая волна (λ = 500 нм) падает нормально на диафрагму с круглым отверстием радиусом r = 0,70 мм. Найти расстояние между двумя наиболее удаленными от диафрагмы точками на оси отверстия, в которых наблюдаются минимумы интенсивности.

543. Плоская монохроматическая световая волна падает нормально на круглое отверстие в диафрагме. На расстоянии L = 9,0 м от нее находится экран, где наблюдается дифракционная картина. Диаметр отверстия уменьшили в 3 раза. Найти новое расстояние от экрана до диафрагмы, при котором число открытых зон Френеля останется прежним.

544. Радиус четвертой зоны Френеля для плоского волнового фронта для некоторой точки наблюдения Р равен r₄ = 3 мм. Определить радиус шестой зоны для той же точки.

545. Определить отношение площадей пятой и шестой зон Френеля для плоского волнового фронта с длиной волны λ = 0,5 мкм, если экран расположен на расстоянии L = 1 м от диафрагмы с круглым отверстием.

546. Найти наименьший радиус круглого отверстия в диафрагме, чтобы при освещении его плоской монохроматической волной в центре дифракционной картины на экране наблюдалось темное пятно. Известно, что радиус третьей зоны Френеля при таком расположении диафрагмы и экрана равен r₃ = 2 мм.

547. Плоская световая волна с длиной волны λ = 600 нм надает нормально на диафрагму с круглым отверстием радиусом r = 1,73 мм. Найти расстояние между двумя наиболее удаленными от диафрагмы точками на оси отверстия, в которых наблюдаются максимумы интенсивности.

548. На диафрагму с круглым отверстием диаметром d = 4 мм падает нормально параллельный пучок монохроматического света (λ = 500 нм). Точка наблюдения находится на оси отверстия на расстоянии L = 1 м от него. Сколько зон Френеля укладывается в отверстии? Будет ли освещена точка наблюдения?

549. На непрозрачную преграду с круглым отверстием радиусом r = 1,0 мм падает плоская монохроматическая световая волна. Когда расстояние от преграды до установленного за ней экрана равно L₁ = 0,575 м, в центре дифракционной картины наблюдается максимум интенсивности. При увеличении расстояния до значения L₂ = 0,862 м максимум интенсивности сменяется минимумом. Определить длину волны света.

550. Плоская световая волна (λ = 600 нм) падает нормально на диафрагму с круглым отверстием радиусом r = 0,60 мм. Найти расстояние между двумя точками на оси отверстия, для которых в отверстии укладывается две и три зоны Френеля.

551. Какое наименьшее число N_min штрихов должна содержать дифракционная решетка, чтобы в спектре второго порядка можно было видеть раздельно две желтые линии натрия с длинами волн λ₁ = 589,0 нм и λ₂ = 589,6 нм? Какова длина такой решетки, если постоянная решетки d = 5 мкм?

552. Две дифракционные решетки имеют одинаковую ширину L = 4 мм, но разные периоды, равные d₁ = 2 мкм и d₂ = 4 мкм. Определить и сравнить их наибольшую разрешающую способность для желтой линии натрия (λ=0,589 нм).

553. Постоянная дифракционной решетки в 4 ра­за больше длины световой волны монохроматического света, нормально падающего на ее поверхность. Определить угол между двумя первыми симметричными дифракционными максимумами.

554. Расстояние между штрихами дифракционной решетки d = 4 мкм. На решетку падает нормально свет с длиной волны λ = 0,58 мкм. Максимум какого наиболь­шего порядка дает эта решетка?

555. На грань кристалла каменной соли падает параллельный пучок рентгеновского излучения. Расстоя­ниемежду атомными плоскостями равно d = 280 пм. Под углом θ = 65° к атомной плоскости наблюдается дифракционный максимум первого порядка. Определить длину волны λ рентгеновского излучения.

556. На кристалл кальцита, расстояние между атомными плоскостями которого d = 0,3 нм, падает пучок параллельных рентгеновских лучей, длина волны которых λ = 0,147 нм. Определить, под каким углом к поверхности кристалла (угол скольжения) должны падать рентгеновские лучи, чтобы наблюдался дифракционный максимум первого порядка.

557. На дифракционную решетку, содержащую N= 600 штрихов на миллиметр, падает нормально белый свет. Спектр проецируется на экран линзой, помещенной вблизи решетки. Определить длину b спектра первого порядка на экране, если расстояние от линзы до экрана L = 1,2 м. Границы видимого спектра: λ_кр = 780 нм, λ_ф=400нм.

558. На щель шириной a = 0,1, мм падает нормально пучок параллельных лучей белого света (λ = 0,38÷0,76 мкм). На экране, отстоящем от щели на расстоянии L=1м, наблюдается дифракционная картина. Найти ширину дифракционного максимума второго порядка.

559. На узкую щель нормально падает монохроматический свет. Угол дифракции для спектра второго порядка φ = 2⁰. Скольким длинам волн падающего света равна ширина щели?

560. На непрозрачную пластину с узкой щелью падает нормально плоская монохроматическая световая волна (λ = 600 нм). Угол отклонения лучей, соответствующих второму дифракционному максимуму, φ = 20°. Определить ширину щели.

561. При прохождении естественного света через два николя, угол между плоскостями поляризации которых α = 45⁰, происходит ослабление света. Коэффициенты поглощения света соответственно в поляризаторе и анализаторе равны k₁ = 0,08 и k₂ = 0,1. Найти, во сколько раз изменилась интенсивность света после прохождения этой системы.

562. Угол между плоскостями пропускания двух одинаковых поляроидов равен α = 50°. Естественный свет, проходя через такую систему, ослабляется в n = 8 раз. Пренебрегая потерей света при отражении, определить коэффициент поглощения k света в поляроидах.

563. Определить постоянную вращения оптически активного вещества, если при введении его между двумя николями, плоскости поляризация которых параллельны, интенсивность света, прошед­шего эту систему, уменьшилась в 5 раз. Толщина слоя оптически активного вещества d = 4 мм. Потерями света на отражение и поглощение пренебречь.

564. Кварцевую пластинку поместили между скрещен­ными николями. При какой наименьшей толщине d_min кварцевой пластины поле зрения между николями будет максимально просветлено? Постоянная вращения кварца равна φ_уд = 27 град/мм.

565. При прохождении света через трубку длиной l₁ = 20 см, содержащую раствор сахара концентрацией С₁ = 10%, плоскость поляризации света повернулась на угол φ₁ = 13,3°. В другом растворе сахара, налитом в трубку длиной l₂ = 15 см, плоскость поляризации повернулась на угол φ₂ = 5,2°. Определить концентрацию С₂ второго раствора.

566. Как изменится интенсивность света, прошедшего два скрещенных поляризатора, если между ними вставить третий поляризатор, плоскость пропускания которого имеет угол равный α = 45⁰ относительно первого? Поглощением и отражением в поляризаторах пренебречь.

567. Луч света переходит из кварца в жидкость, частично отражаясь, частично преломляясь. Отраженный луч максимально поляризован при угле падения α = 43°6’. Определить показатель преломления жидкости и скорость распространения света в ней.

568. Пучок света переходит из жидкости в стекло. Угол падения пучка α = 60°, угол преломления β = 50°. При каком угле падения α_Б пучок света, отраженный от границы раздела этих сред, будет максимально поляризован?

569. Пучок света падает на плоскопараллельную стеклянную пластину, нижняя поверхность которой находится в воде. При каком угле падения α_Б свет, отраженный от границы стекло - вода, будет максимально поляризован?

570. Параллельный пучок света переходит из глицерина в стекло так, что пучок, отраженный от границы раздела этих сред, оказывается максимально поляризованным. Определить угол γ между падающим и преломленным пучками.