Теоретические и эмпирические частоты. Критерии согласия.
Эмпирические частоты получают в результате опыта (наблюдения). Теоретические частоты рассчитывают по формулам. Для нормального закона распределения их можно найти следующим образом:
, (*)
где 
– сумма эмпирических (наблюдаемых) частот; 
– разность между двумя соседними вариантами (то есть длина частичного интервала); 
– выборочное среднее квадратическое отклонение; 
; 
– выборочная средняя арифметическая;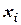 
– середина 
-го частичного интервала; значения функции 
находят по таблице (см. приложения).
Обычно эмпирические и теоретические частоты различаются. Возможно, что расхождение случайно и связано с ограниченным количеством наблюдений; возможно, что расхождение неслучайно и объясняется тем, что для вычисления теоретических частот выдвинута статистическая гипотеза о том, что генеральная совокупность распределена нормально, а в действительности это е так. Распределение генеральной совокупности, которое она имеет в силу выдвинутой гипотезы, называют теоретическим.
Возникает необходимость установить правило (критерий), которое позволяло бы судить, является ли расхождение между эмпирическим и теоретическим распределениями случайным или значимым. Если расхождение окажется случайным, то считают, что данные наблюдений (выборки) согласуются с выдвинутой гипотезой о законе распределения генеральной совокупности и, следовательно, гипотезу принимают. Если же расхождение окажется значимым, то данные наблюдений не согласуются с выдвинутой гипотезой, и её отвергают.
Критерием согласия называют критерий, который позволяет установить, является ли расхождение эмпирического и теоретического распределений случайным или значимым, то есть согласуются ли данные наблюдений с выдвинутой статистической гипотезой или не согласуются.
Имеются несколько критериев согласия: критерий 
(Пирсона), критерий Колмогорова, критерий Романовского и др. Ограничимся описанием того, как критерий применяется к проверке гипотезы о нормальном распределении генеральной совокупности[33] (предлагаем студентам написать рефераты по различным критериям согласия и их применению).
Допустим, что в результате 
наблюдений получена выборка:
| Значения признака | 
| 
| . . . | 
|
| Эмпирические частота | 
| 
| . . . | 
|
| причём | 
|
Выдвинем статистическую гипотезу: генеральная совокупность, из которой извлечена данная выборка, имеет нормальное распределение. Требуется установить, согласуется ли эмпирическое распределение с этой гипотезой. Предположим, что по формуле (*) вычислены теоретические частоты 
. Обозначим 
среднее арифметическое квадратов разностей между эмпирическими и теоретическим частотами, взвешенное по обратным величинам теоретических частот:
.
Чем больше согласуются эмпирическое и теоретическое распределения, тем меньше различаются эмпирические и теоретические частоты и тем меньше значение . Отсюда следует, что характеризует близость эмпирического и теоретического распределений. В разных опытах принимает различные, заранее неизвестные значения, то есть является случайной величиной. Плотность вероятности этого распределения (для выборки достаточно большого объёма) не зависит от проверяемого закона распределения, а зависит от параметра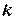 
, называемого числом степеней свободы. Так при проверке гипотезы о нормальном распределении генеральной совокупности 
, где 
– число групп, на которые разбиты данные наблюдений. Существуют таблицы (см. приложения), в которых указана вероятность того, что в результате влияния случайных факторов величина примет значение не меньше вычисленного по данным выборки .
Для определённости примем уровень значимости 0,01. Если вероятность, найденная по таблицам, окажется меньше 0,01, то это означает, что в результате влияния случайных причин наступило событие, которое практически невозможно. Таким образом, тот факт, что приняло значение , нельзя объяснить случайными причинами; его можно объяснить тем, что генеральная совокупность не распределена нормально и, значит, выдвинутая гипотеза о нормальном распределении генеральной совокупности должна быть отвергнута. Если вероятность, найденная по таблицам, превышает 0,01, то гипотеза о нормальном распределении генеральной совокупности согласуется с данными наблюдений и поэтому может быть принята. Полученные выводы распространяются и на другие уровни значимости.
На практике надо, чтобы объём выборки был достаточно большим (
) и чтобы каждая группа содержала 5 – 8 значений признака.
Для проверки гипотезы о нормальном распределении генеральной совокупности нужно:
1) вычислить теоретические частоты по формуле (*);
2) вычислить , где 
– соответственно частоты эмпирические и теоретические;
3) вычислить число степеней свободы , где – число групп, на которые разбита выборка;
4) выбрать уровень значимости;
5) найти по таблице (см. приложения) по найденным 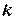и вероятность 
, причём, если эта вероятность меньше принятого уровня значимости, то гипотезу о нормальном распределении генеральной совокупности отвергают; если же вероятность больше уровня значимости, то гипотезу принимают.
ПРИМЕР 5. Проверить, согласуются ли данные выборки со статистической гипотезой о нормальном распределении генеральной совокупности, из которой извлечена выборка:
| варианта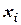
| |||||||||
частота 
|
Решение. Вычислим выборочное среднее и выборочную дисперсию:
; 
.
Далее, вычислим теоретические частоты по формуле (*):
|
|
| 
| 
| 
| 
|
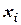
| – 19,7 | – 2,67 | 0,0113 | |||
| – 14,7 | – 1,99 | 0,0551 | |||
| – 9,7 | – 1,31 | 0,1691 | |||
| – 4,7 | – 0,63 | 0,3271 | |||
| 0,3 | 0,05 | 0,3984 | |||
| 5,3 | 0,73 | 0,3056 | |||
| 10,3 | 1,41 | 0,1476 | |||
| 15,3 | 2,09 | 0,0449 | |||
| 20,3 | 2,77 | 0,0086 | |||
| 
|
Найдём 
. Вычислим число степеней свободы, учитывая, что число групп выборки 
. Уровень значимости примем равным 0,01. По таблице (см. приложения) при 
и 
находим вероятность 
; при 
вероятность 
. Используя линейную интерполяцию, получаем приближённое значение искомой вероятности 0,16 > 0,01.
Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.
[1] Эта формула является следствием двух теорем - сложения и умножения.
[2] Хотим заметить, что далеко не всегда властелины были глупыми людьми, не знающими математики. Так, например, Наполеон был немного математиком, интересовался, в частности, геометрией. Он вёл дискуссии с Лагранжем и Лапласом, когда ещё не был правителем Франции. Как-то в одной из таких дискуссий Лаплас резко оборвал Бонапарта: «Менее всего мы хотим от Вас, генерал, урока геометрии». В дальнейшем Лаплас стал его главным военным инженером.
Наполеону приписывают теорему: «Если на сторонах произвольного треугольника во внешнюю сторону построены равносторонние треугольники, то их центры образуют равносторонний треугольник» - это так называемый вешний треугольник Наполеона.
Так же ему приписывают один из знаменитых палиндромов (читается в обе стороны одинаково): «ABLE WAS I ERE I SAW ELBA» - я был силён, пока не увидел Эльбу.
[3] При доказательстве можно воспользоваться приближенной формулой Стирлинга.
[4] Напомню, что счётным является множество, элементы которого можно пронумеровать числами натурального ряда.
[5] - событие, состоящее в том, что случайная величина приняла в опыте значение , причём в одном испытании, как уже отмечалось, случайная величина принимает одно и только одно возможное значение.
[6] Воспользоваться вторым свойством для функции
[7] Происхождение термина «математическое ожидание» связано с начальным периодом возникновения теории вероятностей (XVI-XVII вв.), когда область её применения ограничивалась азартными играми. Игрока интересовало среднее значение ожидаемого выигрыша или, иными словами, математическое ожидание выигрыша.
[8] закон распределения.
[9] Нормальное распределение было найдено впервые Муавром в 1733 г. в связи с исследованием предела биномиального распределения. Открытие прошло незамеченным; только в 1809 г. Гауссом и в 1812 г. Лапласом оно было снова открыто в связи с теорией ошибок наблюдений.
Существует известное замечание Липмана, гласящее, «каждый уверен в справедливости закона ошибок: экспериментаторы – потому, что они думают, что это математическая теорема, математики – потому, что они думают, что это экспериментальный факт».
Отметим, что обе стороны совершенно правы, если только это их убеждение не слишком безусловно: при математическом доказательстве (см.центральную предельную теорему) утверждается, что при некоторых ограничениях вправе ожидать нормальное распределение, а статистический опыт показывает, что в действительности распределения являются часто приближённо нормальными. Поэтому, нормальному распределению уделяется большое внимание.
[10] В этом состоит сущность так называемого правила трёх сигм: если случайная величина распределена нормально, то абсолютная величина её отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.
На практике правило трёх сигм применяется так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведённом правиле, выполняется, то имеются все основания предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.
[11] Применяется в теории надёжности для описания времени безотказной работы невосстанавливаемых изделий.
[12] Есть и другая формулировка: Вероятность того, что отклонение случайной величины Х от её математического ожидания по абсолютной величине меньше положительного числа , не меньше чем , то есть справедливо неравенство .
[13] Напомним, что R
[14] Однако ошибочно думать, что увеличивая число измерений можно достичь сколь угодно большой точности. Дело в том, что сам прибор даёт показания лишь с точностью ; поэтому каждый из результатов измерений, а следовательно и их среднее арифметическое, будут получены лишь с точностью, не превышающей точности прибора.
[15] Доказательство впервые было опубликовано в 1713 году.
[16] Доказательство, предложенное Я.Бернулли, было сложным; более простое доказательство было дано П.Чебышевым в 1846 году.
[17] Известно, что произведение двух сомножителей, сумма которых есть величина постоянная, имеет наибольшее значение при равенстве сомножителей.
[18] Одномерную случайную величину иногда называют скалярной случайной величиной.
[19] Интегральная функция распределения.
[20] Дифференциальная функция распределения.
[21] Предполагается, что интегральная функция распределения вероятностей имеет непрерывную смешанную частную производную второго порядка.
[22] Мы записали условные законы распределения случайной величины при условии, что другая случайная величина приняла определённое значение.
[23] Предлагаем все дальнейшие вычисления сделать самостоятельно.
[24] Полученный ряд называется ранжированным.
[25] Заметим, что в теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике – соответствие между наблюдаемыми вариантами и их частотами, или относительными частотами.
[26] строится аналогично полигону в прямоугольной системе координат.
[27] или простое среднее отклонение.
[28] Данное распределение называют выборочным.
[29] Полученные выводы применимы и для бесповторной выборки, если её объём значительно меньше объёма генеральной совокупности. Это положение часто используется на практике.
[30] Интервал имеет случайные концы (их называют доверительными границами). Действительно, в разных выборках получаются различные значения . Следовательно от выборки к выборке будут изменяться и концы доверительного интервала, то есть доверительные границы сами являются случайными величинами – функциями от . Так как случайной величиной является не оцениваемый параметр , а доверительный интервал, то более правильно говорить не о вероятности попадания в доверительный интервал, а о вероятности того, что доверительный интервал покроет .
[31] Обычно при выполнении пп. 4 – 7 используют статистику с нормальным распределением, статистику Стьюдента, Фишера.
[32] То есть – с математическим ожиданием.
[33] Критерий применяется аналогично и для других распределений