Решение.

1-й способ:

Если бензоколонку поставить на середине шоссе, то есть на 50-м километре (средняя арифметическая), то пробеги с учётом числа поездок составят

- в одном направлении:

;

- в противоположном:

Общий пробег в оба направления окажется равным 5390 км.

2-й способ:

Уменьшения пробега можно достичь, если бензоколонку поставить на 63,85-м километре, то есть на среднем участке шоссе с учётом числа поездок (средняя арифметическая взвешенная). В этом случае пробеги составят по 2475,75 км в оба направления. Таким образом, общий пробег составит 4951,5 км и окажется меньше, чем в первом способе решения, на 438,5 км.

3-й способ:

Наилучший результат, то есть минимальный общий пробег, получим, если поставить бензоколонку на 78-м километре, что будет соответствовать медиане. Заметим, что медиана вычислена по формуле: . При этом вариационный ряд записываем в виде

Следовательно . Тогда пробеги составят 3820 км и 990 км соответственно. Общий пробег, в этом случае, равен 4810 км, то есть он оказался меньше общих пробегов, рассчитанных в предыдущих способах.

Модой () называется варианта, наиболее часто встречающаяся в данном вариационном ряду. Для дискретного ряда мода, являющаяся характеристикой вариационного ряда, определяется по частотам вариант и соответствует варианте с наибольшей частотой. В случае интервального распределения с равными интервалами, модальный интервал (то есть интервал, содержащий моду) определяется по наибольшей частоте, а при неравных интервалах – по наибольшей плотности. Мода рассчитывается по формуле:

где – нижняя граница модального интервала; 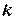– величина модального интервала; – частота модального интервала; – частота интервала, предшествующего модальному; – частота интервала, следующего за модальным.

Вариационные ряды, в которых частоты вариант, равноотстоящих от средней, равны между собой, называются симметричными. Особенность симметричны вариационных рядов состоит в равенстве трёх характеристик – средней арифметической, моды и медианы, то есть:

(это необходимое, но не достаточное, условие симметричности вариационного ряда).

Вариационные ряды, в которых расположение вариант вокруг средней не одинаково, то есть частоты по обе стороны от средней изменяются по-разному, называются асимметричными, или скошенными. Различают асимметрию – левостороннюю и правостороннюю.

Средние величины, характеризую вариационный ряд одним числом, не учитывают вариацию признака, между тем эта вариация существует. Для измерения вариации признака в математической статистике применяют ряд способов.

Вариационный размах (), или широта распределения, есть разность между наибольшим и наименьшим значениями вариационного ряда:

Вариационный размах представляет собой величину неустойчивую, чрезвычайно зависящую от случайных обстоятельств; применяется для приблизительной оценки вариации.

Среднее линейное отклонение[27] (обозначается ) представляет собой среднюю арифметическую из абсолютных значений отклонений вариант от средней. В зависимости от отсутствия или наличия частот вычисляют среднее линейное отклонение невзвешенное или взвешенное:

Средний квадрат отклонения, или дисперсия (обозначается ) наиболее часто применяется как мера колеблемости признака. Дисперсии невзвешенную и взвешенную вычисляют по формулам:

Таким образом, дисперсия есть средняя арифметическая из квадратов отклонений вариант от их средней арифметической.

Квадратный корень из дисперсии называется среднеквадратическим отклонением.

Обобщающими характеристиками вариационных рядов являются моменты распределения. Характер распределения можно определить с помощью небольшого количества моментов.

Средняя из 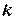- х степеней отклонений вариант от некоторой постоянной величины (ложный ноль) называется моментом 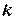-го порядка:

При расчёте средних в качестве весов можно использовать частоты, относительные частоты или вероятности. При использовании в качестве весов частот или относительных частот моменты называются эмпирическими, а при использовании вероятностей – теоретическими. Порядок момента определяется величиной 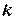. Эмпирический момент 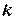-го порядка находится как отношение суммы произведений 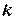-х степеней отклонений вариант от постоянной величины на соответствующие частоты к сумме частот (объём выборки), то есть

В зависимости от выбора постоянной величины различают следующее моменты:

1. Если , то моменты называются начальными. Будем обозначать их через и вычислять по формуле:

Тогда:

- при получаем начальный момент нулевого порядка ;

- при получаем начальный момент первого порядка ;

- при получаем начальный момент второго порядка ;

- при получаем начальный момент третьего порядка ;

- при получаем начальный момент четвёртого порядка ;

и так далее. На практике чаще всего используют моменты первых четырёх порядков.

2. Если (– начало отсчёта), то моменты называются начальными относительно , обозначаются и рассчитываются по формуле:

3. Если (– средняя), то моменты называются центральными, обозначаются и вычисляются так:

Тогда:

- при получаем центральный момент нулевого порядка ;

- при получаем центральный момент первого порядка ;

- при получаем центральный момент второго порядка (служит мерой колеблемости признака);

- при получаем центральный момент третьего порядка

который служит мерой асимметрии распределения признака. Так, если распределение симметрично, то ;

- при получаем центральный момент четвёртого порядка

Коэффициентом асимметрии называется отношение центрального момента третьего порядка к кубу среднеквадратического отклонения:

Если полигон вариационного ряда скошен, то есть одна из его ветвей, начиная от вершины, зримо короче другой, то такой ряд называют асимметричным.

Эксцессом называют уменьшенное на три единицы отношение центрального момента четвёртого порядка к четвёртой степени среднеквадратического отклонения:

Кривые распределения, у которых , менее крутые, имеют более плоскую вершину и называются плосковершинными. Кривые распределения, у которых , более крутые, имеют более острую вершину и называются островершинными.