Теорема Бернулли

Закон больших чисел

ЛЕКЦИЯ 11

 

(продолжение)

 

 

 

Пусть производится независимых испытаний, в каждом из которых вероятность появления события А равна р. Другими словами, пусть имеет место схема Бернулли. Можно ли предвидеть какова будет примерно относительная частота появлений события? Положительный ответ на этот вопрос даёт теорема, доказанная Я.Бернулли[15], которая получила название «закона больших чисел» и положила начало теории вероятностей как науки[16].

 

ТЕОРЕМА Бернулли: Если в каждом из независимых испытаний, проводимых в одинаковых условиях, вероятность р появления события А постоянна, то относительная частота появления события А сходится по вероятности к вероятности р – появления данного события в отдельном опыте, то есть

.

 

Доказательство. Итак, имеет место схема Бернулли, . Обозначим через дискретную случайную величину – число появлений события А в -ом испытании. Ясно, что каждая из случайных величин может принимать лишь два значения: 1 (событие А наступило) с вероятностью р и 0 (событие А не наступило) с вероятностью , то есть

 

()
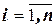Р	р

 

Нетрудно найти

 

,

 

.

 

Можно ли применить к рассматриваемым величинам теорему Чебышева? Можно, если случайные величины попарно независимы и дисперсии их равномерно ограничены. Оба условия выполняются. Действительно, попарная независимость величин следует из того, что испытания независимы. Далее[17] при и, следовательно, дисперсии всех величин ограничены, например числом . Кроме того, заметим, что каждая из случайных величин при появлении события А в соответствующем испытании принимает значение, равное единице. Следовательно, сумма равна числу - появлений события А в испытаниях, а значит

 

,

 

то есть дробь равна относительной частоте появлений события А в испытаниях.

 

Тогда, применяя теорему Чебышева к рассматриваемым величинам, получим:

 

,

 

что и требовалось доказать.

 

 

Замечание 1: Теорема Бернулли является простейшим частным случаем теоремы Чебышева.

 

Замечание 2: На практике часто неизвестные вероятности приходится приближённо определять из опыта, то для проверки согласия теоремы Бернулли с опытом было проведено большое число опытов. Так, например, французский естествоиспытатель XVIII века Бюффон бросил монету 4040 раз. Герб выпал при этом 2048 раз. Частота появления герба в опыте Бюффона приближённо равна 0,507. Английский статистик К.Пирсон бросал монету 12 000 раз и при этом наблюдал 6019 выпадений герба. Частота выпадения герба в этом опыте Пирсона равна 0,5016. В другой раз он бросил монету 24 000 раз, и герб при этом выпал 12 012 раз; частота выпадения герба при этом оказалась равной 0,5005. Как видим, во всех приведённых опытах частота лишь немного уклонилась от вероятности 0,5 – появления герба в результате одного бросания монеты.

 

Замечание 3: Было бы неправильным на основании теоремы Бернулли сделать вывод, что с ростом числа испытаний относительная частота неуклонно стремится к вероятности р; другими словами, из теоремы Бернулли не вытекает равенство . В теореме речь идёт лишь о вероятности того, что при достаточно большом числе испытаний относительная частота будет как угодно мало отличаться от постоянной вероятности появления события в каждом испытании. Таким образом, сходимость относительной частоты к вероятности р отличается от сходимости в смысле обычного анализа. Для того чтобы подчеркнуть это различие, вводят понятие «сходимости по вероятности». Точнее, различие между указанными видами сходимости состоит в следующем: если стремится при к р как пределу в смысле обычного анализа, то, начиная с некоторого и для всех последующих значений , неуклонно выполняется неравенство ; если же стремится по вероятности к р при , то для отдельных значений неравенство может и не выполняться.