Распределение Гаусса (нормальное распределение)
Наиболее известным и часто применяемым в теории вероятностей законом является нормальный закон распределения или закон Гаусса[9].
Главная особенность нормального закона распределения заключается в том, что он является предельным законом для других законов распределения.
|
Будем говорить, что непрерывная случайная величина Х, принимающая значения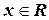 
, подчиняется нормальному закону, если её плотность распределения (дифференциальная функция) имеет вид
.
Нетрудно видеть, что нормальное распределение определяется двумя параметрами: 
и 
. Достаточно задать эти параметры, чтобы задать нормальное распределение.
|
Заметим, что для нормального распределения интегральная функция имеет вид:
.
Покажем теперь, что вероятностный смысл параметров и таков: а есть математическое ожидание, 
– среднее квадратическое отклонение (то есть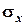 
) нормального распределения:
а) по определению математического ожидания непрерывной случайной величины имеем
Действительно
,
так как под знаком интеграла стоит нечётная функция, и пределы интегрирования симметричны относительно начала координат;
- интеграл Пуассона.
Итак, математическое ожидание нормального распределения равно параметру а.
б) по определению дисперсии непрерывной случайной величины и, учитывая, что 
, можем записать
.
Интегрируя по частям, положив 
, найдём
Следовательно 
.
Итак, среднее квадратическое отклонение нормального распределения равно параметру .
|
В случае если 
и 
нормальное распределение называют нормированным (или, стандартным нормальным) распределением. Тогда, очевидно, нормированная плотность (дифференциальная) и нормированная интегральная функция распределения запишутся соответственно в виде:
(Функция 
, как вам известно, называется функцией Лапласа (см. ЛЕКЦИЮ5) или интегралом вероятностей. Обе функции, то есть 
, табулированы и их значения записаны в соответствующих таблицах).
Свойства нормального распределения (свойства нормальной кривой):
1. Очевидно, функция 
на всей числовой прямой.
2. 
, то есть нормальная кривая расположена над осью Ох.
3. 
, то есть ось Ох служит горизонтальной асимптотой графика.
4. Нормальная кривая симметрично относительно прямой х = а (соответственно график функции 
симметричен относительно оси Оу). Следовательно, можем записать: 
.
5. 
.
6. Легко показать, что точки 
и 
являются точками перегиба нормальной кривой (доказать самостоятельно).
7. Очевидно, что
но, так как 
, то 
. Кроме того 
, следовательно, все нечётные моменты равны нулю. Для чётных же моментов можем записать:
8. 
.
9. 
.
10. 
, где 
.
11. При отрицательных значениях случайной величины: 
, где .
12. 
.
13. Вероятность попадания случайной величины на участок, симметричный относительно центра распределения, равна:
ПРИМЕР 3.Показать, что нормально распределённая случайная величина Х отклоняется от математического ожидания М(Х) не более чем на 
.
Решение. Для нормального распределения: 
. Далее, запишем:
Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0, 0027. Это означает, что лишь в 0,27% случаев так может произойти. Такие события, исходя из принципа невозможности маловероятных событий, можно считать практически невозможными[10].
Итак, событие с вероятностью 0,9973 можно считать практически достоверным, то есть случайная величина отклоняется от математического ожидания не более чем на .
ПРИМЕР 4.Зная характеристики нормального распределения случайной величины Х – предела прочности стали: 
кг/мм2 и 
кг/мм2, найти вероятность получения стали с пределом прочности от 31 кг/мм2 до 35 кг/мм2.
Решение.
.
3. Показательное распределение (экспоненциальный закон распределения)[11]
|
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х, которое описывается дифференциальной функцией (плотность распределения)
где 
- постоянная положительная величина.
Показательное распределение определяется одним параметром . Эта особенность показательного распределения указывает на его преимущество, по сравнению с распределениями, зависящими от большего числа параметров. Обычно параметры неизвестны и приходится находить их оценки (приближённые значения); разумеется, проще оценить один параметр, чем два, или три и т.д.
|
Нетрудно записать интегральную функцию показательного распределения:
Мы определили показательное распределение при помощи дифференциальной функции; ясно, что его можно определить, пользуясь интегральной функцией.
Замечание: Рассмотрим непрерывную случайную величину Т – длительность времени безотказной работы изделия. Обозначим принимаемые её значения через t, 
. Интегральная функция распределения 
определяет вероятность отказа изделия за время длительностью t. Следовательно, вероятность безотказной работы за это же время, длительностью t, то есть вероятность противоположного события 
, равна
.
Функцией надёжности 
называют функцию, определяющую вероятность безотказной работы изделия (элемента) за время длительностью t. Если длительность времени безотказной работы изделия (элемента) имеет показательное распределение, то функция надёжности, в этом случае, запишется в виде
.
Таким образом, показательным законом надёжности называют функцию надёжности, определяемую последним равенством, где - интенсивность отказов.
Свойства показательного распределения:
1. Математическое ожидание показательного распределения равно обратной величине параметра , то есть 
. Действительно
.
2. 
, следовательно 
. Таким образом, математическое ожидание и среднее квадратическое отклонение показательного распределения равны между собой.
3. 
.
4. 
.
5. 
.
ПРИМЕР 4.Пусть время, необходимое для ремонта станков, распределено по показательному (экспоненциальному) закону с параметром 
. Определить вероятность того, что время ремонта одного станка меньше 6-и часов. Найти среднее время ремонта одного станка.
Решение. Т – время ремонта станка 
. Тогда можем записать:
.
Далее, так как среднее время ремонта – это М( Т ), то
(часа).