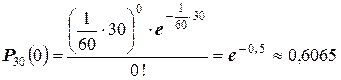Распределение Пуассона (закон редких событий)

Основные законы распределения случайной величины

ЛЕКЦИЯ 9

 

(продолжение)

Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А равна р. Для определения вероятности k – появлений события А в этих испытаниях используют, как вам уже известно, формулу Бернулли. Однако, как быть если n велико, а вероятность р события А достаточно мала (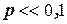)[8]. В таких случаях прибегают к асимптотической формуле Пуассона.

Итак, поставим своей задачей найти вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно k раз.

Сделаем важное допущение: пусть произведение 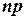сохраняет постоянное значение, а именно . Это означает, что среднее число появлений события в различных сериях испытаний, то есть при различных значениях n, остаётся неизменным.

Воспользуемся формулой Бернулли для вычисления интересующей нас вероятности:

 

 

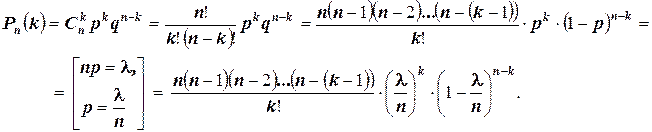
Приняв во внимание, что n имеет очень большое значение, вместо найдём . При этом будет найдено лишь приближённое значение отыскиваемой вероятности: n хотя и велико, но всё же конечно, а при отыскании предела мы устремим n к бесконечности.

Итак

 

 

В результате (для простоты записи знак приближённого равенства опущен) запишем

 

.

 

Эта формула выражает закон распределения Пуассона вероятностей массовых (n велико) редких (р мало) событий.

 

Таким образом, будем говорить, что дискретная случайная величина , принимающая счётное множество значений, подчиняется закону распределения Пуассона, если вероятности её возможных значений задаются выражением:

.

 

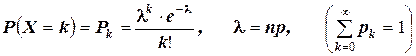Свойства распределения Пуассона:

1. .

 

Действительно:

 

 

2. .

 

3. если , то из биномиального распределения следует закон распределения Пуассона.

ПРИМЕР 1.Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что на базу прибудут: а) три негодных изделия; б) не более трёх повреждённых изделия.

Решение: по условию n=5000, p=0,0002. Найдём .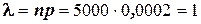

а) k = 3. Искомая вероятность по формуле Пуассона приближённо равна

 

.

 

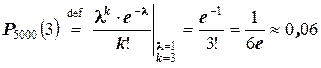б) Пусть случайная величина Х – число изделий, повреждённых в пути, то есть 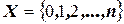. Очевидно, что данная случайная величина распределена по биномиальному закону. Следовательно, искомую вероятность можно вычислить по формуле

 

.

 

Но, так как , то по свойству 3о можем воспользоваться законом распределения Пуассона, то есть, можем записать:

 

.

 

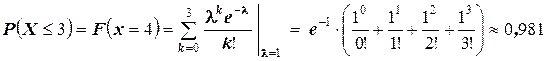Замечание.По формуле Пуассона можно вычислить вероятность того, что число событий, происшедших за время равно 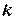, если события образуют пуассоновский поток, причём – интенсивность потока, то есть среднее число событий, которые появляются в единицу времени:

 

.

 

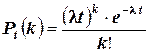ПРИМЕР 2. В течение часа коммутатор получает в среднем 60 вызовов. Какова вероятность того, что за время 30 сек, в течении которых телефонистка отлучилась, не будет ни одного вызова?

Решение: Найдём, прежде всего, – среднее число вызовов за 1 секунду:

 

.

 

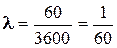Тогда, при 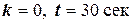, получим: