Биномиальное распределение

 

Биномиальное распределение вероятностей является самым распространённым распределением для дискретных случайных величин.

Итак, пусть производится n независимых испытаний, в каждом из которых событие А может появиться, либо не появиться. И пусть, вероятность наступления события во всех испытаниях постоянна и равна р (следовательно, вероятность непоявления ). Рассмотрим в качестве дискретной случайной величины Х – число появлений события А в этих испытаниях.

Поставим перед собой задачу: найти закон распределения величины Х. Для её решения требуется определить возможные значения случайной величины Х и их вероятности.

Очевидно, событие А в n испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза, . . . , либо n раз. Таким образом, нетрудно записать возможные значения случайной величины 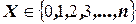. Остаётся найти вероятности этих возможных значений, для чего достаточно воспользоваться формулой Бернулли (см. Лекцию 5):

 

, где k = 0,1,2,…,n.

 

Формула Бернулли и является аналитическим выражением искомого закона распределения.

 

Биномиальным называют распределение вероятностей дискретной случайной величины, определяемое формулой Бернулли.

 

Запишем биномиальный закон в виде таблицы:

 

Х				. . .	k	. . .	n – 1	n
р				. . .		. . .

 

 

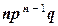
Свойства биномиального распределения:

 

1. .

 

Действительно:

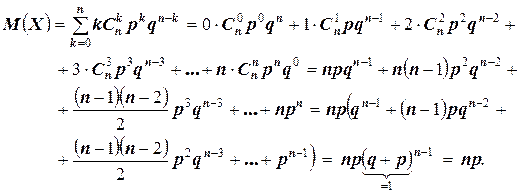
2. (заметим, что 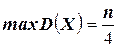при 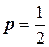) (доказать самостоятельно)

 

3. .

 

 

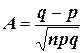4. .

ПРИМЕР 4.Имеется три станка, коэффициент использования по времени которых составляет 0,8. Определить вероятность того, что в середине рабочей смены при нормальных условиях производства из данных трёх станков будет работать не более двух.

Решение. Работа каждого станка – события независимые. Вероятность того, что станок будет работать равна р=0,8 (следовательно q=1-0,8=0,2). Пусть случайная величина Х - число одновременно работающих станков, то есть . Очевидно, что вероятности значений случайной величины Х подчиняются биномиальному закону распределения с параметрами р=0,8; q=0,2; n=3. Значит

 

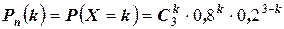, k = 0,1,2,3.

 

Требуется определить вероятность 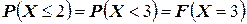. По определению

 

.

 

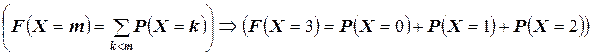Так как:

 

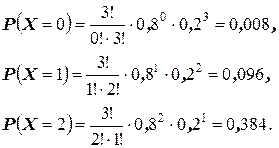
Тогда

 

.
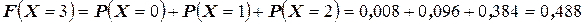