Равномерное распределение непрерывной случайной величины.

 

Непрерывная случайная величина подчиняется равномерному закону распределения, если её возможные значения лежат в некотором определённом интервале, в пределах которого все значения равновероятны, то есть обладают одной и той же плотностью вероятности. Другими словами, распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, дифференциальная функция имеет постоянное значение.

Случайные величины, имеющие равномерное распределение вероятностей, часто встречаются на практике. Например, при снятии показаний измерительных приборов. Ошибка при округлении отсчёта до ближайшего целого деления шкалы является случайной величиной, которая может с постоянной плотностью вероятности принимать любые значения между двумя соседними делениями. Таким образом, данная случайная величина имеет равномерное распределение.

Найдём дифференциальную функцию (плотность) равномерного распределения, считая, что все возможные значения случайной величины Х заключены в промежутке , на котором дифференциальная функция сохраняет постоянное значение, то есть .

По условию Х не принимает значений вне промежутка , поэтому при всех 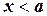и .

Найдём значение постоянной С. Так как все возможные значения случайной величины принадлежат промежутку , то справедливо:

 

.

 

Итак, закон равномерного распределения случайной величины на отрезке (здесь ) аналитически можно записать так:

 

 

 

Найдём теперь интегральную функцию равномерного распределения непрерывной случайной величины. Для этого воспользуемся формулой

 

.

 

Тогда:

- если 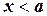, то и, следовательно, ;

- если , то и, следовательно

 

.

 

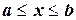- если , то .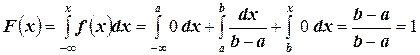

 

Итак, искомая интегральная функция распределения аналитически может быть записана так:

 

 

 

Свойства равномерного непрерывного распределения:

 

1. ;

 

2. ;

3. моды распределение не имеет;

 

 

5. ;

 

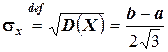6. В силу симметрии распределения все нечётные моменты равны нулю.

 

.

 

Тогда

 

.

 

7. .

 

ПРИМЕР 2.Троллейбусы идут строго по расписанию и с интервалом в 6 мин. Найти вероятность того, что пассажир, подошедший к остановке, будет ожидать троллейбус менее двух минут.

Решение. Время ожидания троллейбуса есть непрерывная случайная величина Х, имеющая равномерное распределение на промежутке [0,6], так как с равной вероятностью время ожидания может быть любым в этом промежутке. Тогда

 

 

Тогда

 

.