Теорема Муавра - Лапласа (локальная)

Формула Бернулли (схема повторения опытов)

Повторение испытаний

ЛЕКЦИЯ 5

Опыты называются независимыми , если вероятность того или иного исхода каждого опыта не зависит от того, какие исходы имели другие опыты. Независимые опыты могут проводиться как в одинаковых условиях, так и в различных. В первом случае вероятность появления какого - либо события во всех опытах одна и та же, во втором случае - она меняется от опыта к опыту.

Ниже мы воспользуемся понятием сложного события, понимая под ним совмещение нескольких отдельных событий, которые называют простыми.

Итак, пусть производится независимых опытов в одинаковых условиях, в каждом из которых некоторое событие может произойти с одной и той же вероятностью . Причём, каждый опыт (испытание) имеет лишь два исхода: событие может появиться (произойти), либо не появиться. Условно, появление события будем рассматривать как успех, а его не наступление (т.е. событие ) - как неудачу. Следовательно, вероятность не наступления события в каждом испытании также постоянна и равна . Данная ситуация, или данная схема проведения опытов называется схемой Бернулли. Итак, еще раз:

схемой Бернулли называется последовательность независимых испытаний, проводимых при одних и тех же условиях, в каждом из которых событие либо происходит с постоянной вероятностью , не зависящей от номера испытания, либо не происходит с вероятностью (здесь ).

Ставятся задачи:

Задача №1. Найти вероятность того, что в схеме Бернулли из испытаний событие произойдет ровно 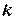раз () и, следовательно, не осуществится раз.

Задача № 2. Найти вероятность того, что в схеме Бернулли из испытаний событие произойдет не менее и не более раз , где и заданы.

Задача № 3. Найти наивероятнейшее число появления события в схеме Бернулли из испытаний, при котором достигает наибольшего значения.

Решение №1.

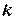Вероятность не зависит от номера испытания и, что также важно, не требуется чтобы событие повторилось ровно раз в определенной последовательности. Предположим, для определенности, что событие произойдет подряд 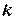раз, а в остальных испытаниях - не произойдет. Используя теорему об умножении вероятностей, можем в этом случае записать:

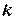Таких несовместных событий столько, сколько сочетаний из элементов по элементов в каждом. Поэтому по теореме о вероятности суммы несовместных событий получим формулу, называемую формулой Бернулли:

Заметим, что .

Легко видеть, что вероятность , вычисленная по формуле Бернулли, является коэффициентом при в разложении бинома , поэтому вероятность называется биномиальной, а функция - производящей функцией для распределения вероятностей в схеме Бернулли из испытаний. Разложение бинома Ньютона имеет вид:

Члены этого разложения, с учетом формулы Бернулли, запишем в таблицу

k				. . .	k	. . .	n
				. . .		. . .

которую называют биномиальным законом распределения вероятностей события в испытаниях схемы Бернулли.

Заметим, что вероятность хотя бы одного появления события в испытаниях схемы Бернулли равна: . Кстати,подумайте над следующим вопросом: честное ли пари вам прелагают, если вы выиграете в том случае, когда при 24-х кратном бросании двух игральных костей хотя бы один раз одновременно появятся две шестёрки? Ответ дайте в конце пары.

(РЕШЕНИЕ. Вероятность одновременного выпадения двух шестерок при одном подбрасывании равна , следовательно - не выпадения равна . Нетрудно видеть, что испытания, т.е. подбрасывания двух игральных костей 24 раза, удовлетворяют схеме Бернулли, следовательно вероятность одновременного появления двух шестерок хотя бы один раз равна .То есть, пари нечестное.)

Другие примеры на применение формулы Бернулли, рассмотрим немного позднее, а именно после того, как решим задачи № 2 и № 3.

Решение № 2.

Нетрудно показать, что вероятность того, что в схеме Бернулли из испытаний событие произойдет не менее и не более раз , где и заданы, может быть вычислена по формуле:

Решение № 3

Важной является задача № 3 о наивероятнейшем числе появления события в схеме Бернулли из испытаний.

Рассмотрим отношение:

Из полученного следует, что:

1) если Z, то , т.е. существует два максимума;

2) если Z, то , где - целая часть числа , тогда .

Таким образом, в общем случае можем записать:

ПРИМЕР 1. При некоторых условиях стрельбы вероятность попадания в цель при одном выстреле равна . Произведено выстрела.

а). Каково наивероятнейшее число попаданий в цель?

б). Какова его вероятность?

в). Какова вероятность двух попаданий?

г). Какова вероятность хотя бы одного попадания?

Решение.

а). Так как .

б). .

в). .

г). .

ПРИМЕР 2. Некто Сэмюэль Пепайс обратился к Исааку Ньютону с вопросом: какое из событий наиболее вероятно -

n появление по крайней мере одной «шестерки» при подбрасывании 6-ти игральных костей;

n хотя бы двух «шестерок» при подбрасывании 12-ти;

n хотя бы трех «шестерок» при подбрасывании 18-ти?

Решение.

Вероятность непоявления «шестерки» при одном подбрасывании, как известно, равна , следовательно, при шести подбрасываниях равна . Таким образом, вероятность появления по крайней мере одной «шестерки» при подбрасывании 6-ти игральных костей может быть найдена по формуле:

Событие «хотя бы две» противоположно событию «либо ни разу, либо один раз», т.е.

Событие «хотя бы три» противоположно событию «либо ни разу, либо один раз, либо два раза», т.е.

Таким образом, как видим, предпочтительнее первая стратегия – таким и был ответ Ньютона.

Замечу, что при больших значениях числа испытаний в схеме Бернулли формула для подсчета становится громоздкой для вычислений. В этих случаях пользуются асимптотическими формулами.

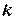Рассмотрим асимптотическую формулу Пуассона, которая справедлива при малых и больших (распределение редких событий в схеме Бернулли). Другими словами рассматривается как функция трех переменных , при условии, что - фиксировано, а меняются ( именно так, что ).

ТЕОРЕМА Пуассона[3]. Пусть так, что . Тогда в схеме Бернулли

или, то же самое

Доказательство.

Что и требовалось доказать.

Следствие: при указанных выше условиях, т.е. при и справедлива приближенная формула Пуассона:

ПРИМЕР. Телефонная станция обслуживает 800 абонентов. Для каждого абонента вероятность того, что в течении часа он позвонит на станцию равна =0,01. Найти вероятность того, что четыре абонента позвонят на станцию в течении часа.

Решение. .

Остановлюсь еще на двух предельных теоремах в схеме Бернулли - локальной теореме Муавра - Лапласа (её доказательство получим как частный случай закона больших чисел - предельной теоремы Ляпунова, доказательство которой нам ещё предстоит провести) и интегральной теореме Муавра - Лапласа. Итак:

· локальная приближенная формула Лапласа (при больших )

причем, во-первых, погрешность этой формулы есть величина порядка , во-вторых, для функции составлена таблица её значений. Для отрицательных значений аргумента пользуются той же таблицей, так как, очевидно, , то есть функция четная. Заметим также, что график функции называется кривой Гаусса (см. рис.).

· интегральная приближенная формула Лапласа ( при больших , т.е. ; ):

где

Для функции также есть табличные значения, когда . При справедливо неравенство , что равносильно условию (график функции см. на рис.). Отметим, что точность растет с ростом произведения , и, обычно, пользуются этими формулами в случае, когда .

Замечание: если функция Лапласа записана в виде , то . Иногда функция Лапласа может быть записана в виде

тогда .

Отметим, что в схеме Бернулли рассматривались независимые испытания. Если же вероятность наступления события в 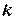-ом опыте зависит от результата только предыдущего, - ого опыта, то такая схема называется цепью Маркова.