Нужно записать шесть уравнений статики

∑х = 0, ∑у = 0, ∑z = 0,

∑M_x = 0, ∑M_y = 0, ∑M_z = 0.

Из них три дают тождество 0 = 0. Остаются три уравнения

∑х = 0, ∑M_y = 0, ∑M_z = 0.

Запишем их по порядку, подставляя σ по формуле (5.13).

. (5.14)

Поскольку , , а это статический момент сечения относительно нейтральной линии.

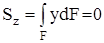. (5.15)

.

Рис.5.16

По той же причине, что и в предыдущем уравнении 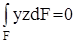. Это другая геометрическая характеристика сечения – центробежный момент инерции

. (5.16)

На основании равенства (5.15) заключаем, что ось z – нейтральная линия сечения – проходит через центр тяжести поперечного сечения. Равенство (5.16) показывает, что оси y и z – главные центральные оси сечения. Этим определяется положение нейтральной линии сечения.

Таким образом, если силовая линия совпадает с одной из главных центральных осей сечения, то изгиб будет плоским и нейтральная линия сечения совпадает с другой главной центральной осью.

Из третьего уравнения (5.13) определим радиус кривизны нейтрального слоя.

.

Вспомнив, что , представляет собой момент инерции сечения относительно оси z, можем последнюю формулу записать в виде

. (5.17)

Наконец, подставив формулу (5.17) в выражение (5.13), получим формулу для нормального напряжения при чистом изгибе

. (5.18)

Формула (5.17) в приведённом выводе была вспомогательной, однако она имеет и большое самостоятельное значение. Её можно трактовать как закон Гука при изгибе, поскольку она связывает деформацию (кривизну нейтрального слоя 1/ρ) с действующим изгибающим моментом.

Произведение EJ носит название жёсткости сечения при изгибе и имеет размерность кН×см².