Тема 5. Выборочное наблюдение
Под выборочным наблюдением понимается метод исследования, связанный с установлением обобщающих показателей совокупности по некоторой ее части на основе метода случайного отбора. При выборочном наблюдении обследованию подвергается сравнительно небольшая часть всей совокупности (10 – 15%). Вся совокупность, подлежащая обследованию, называется генеральной совокупностью. Отобранная из генеральной совокупности часть единиц, непосредственно подвергающаяся обследованию, называется выборочной совокупностью или выборкой
В связи с тем, что исследуемая совокупность состоит из единиц с варьирующими признаками, состав выборки может отличаться от состава генеральной совокупности, вызывая расхождение между генеральными и выборочными характеристиками. Такие расхождения называются ошибками репрезентативности или ошибками выборки.
При использовании выборочного наблюдения можно установить две характеристики выборочной совокупности: среднее значение признака и долю единиц совокупности, обладающих альтернативным признаком.
Доля единиц, обладающих альтернативным признаком, в генеральной совокупности определяется следующим образом:
 (83)
(83)
где Р – доля альтернативного признака в генеральной совокупности;
Na – численность единиц, обладающих альтернативным признаком, в генеральной совокупности;
N – общая численность единиц в генеральной совокупности.
В выборочной совокупности доля единиц, обладающих альтернативным признаком, определяется аналогично:
 (84)
(84)
Так, если в ходе выборочного наблюдения качества рыбных консервов было установлено, что из 5000 обследованных банок 22 были признаны бракованными. В этом случае доля бракованной продукции (доля единиц, обладающих альтернативным признаком) в выборочной совокупности составит:
 или 2,44%
или 2,44%
Характеристики, полученные при выборочном обследовании, будут отличаться от характеристик генеральной совокупности на величину ошибки выборочной средней и ошибки доли альтернативного признака.
Величина ошибки репрезентативности и методика ее расчета зависит от используемого вида выборочного наблюдения, от способа формирования выборочной совокупности (повторный или бесповторный отбор), а также от объема выборки. Различают два вида ошибок – среднюю и предельную.
В статистике используется понятие малой выборки, которое не связано с особенностями формирования выборочной совокупности, а только с тем, что ее численность не превышает 30 единиц. Ошибка выборки в этом случае будет заведомо больше и для ее расчета используются специальные формулы.
В таблице 4 приведены основные виды формул, используемых для расчета средней ошибки выборки и средней ошибки доли альтернативного признака.
Таблица 4. - Формулы для расчета средней ошибки репрезентативности
| Вид отбора и объем выборочной совокупности | Средняя ошибка выборочной средней | Средняя ошибка доли альтернативного признака | ||
| Формула | Номер формулы | Формула | Номер формулы | |
| Повторный отбор (бесповторный объемом до 5%) | 
| (85) | 
| (86) |
| Бесповторный отбор объемом свыше 5% | 
| (87) | 
| (88) |
| Малая выборка | 
| (89) | 
| (90) |
где N - объем генеральной совокупности.
На основе средней ошибки выборки можно определить пределы среднего значения признака и пределы доли альтернативного признака в генеральной совокупности.
Пределы генеральной средней находятся по формуле:
 (91)
(91)
где 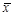 - генеральная средняя;
- генеральная средняя;
 - выборочная средняя.
- выборочная средняя.
Пределы доли альтернативного признака в генеральной совокупности:
 (92)
(92)
где Р – генеральная доля альтернативного признака.
Однако, средняя ошибка выборки совпадает с реальной только в 683 случаях из 1000. Если хотят получить результат с большей надежностью, используют предельную ошибку репрезентативности. Для ее определения среднюю ошибку увеличивают в t раз, где t - коэффициент доверия.
 (93)
(93)
где Δ - предельная ошибка репрезентативности;
t - коэффициент доверия;
μ - средняя ошибка репрезентативности.
Подставляя в выражение (93) значение средней ошибки выборочной средней из таблицы 4, можно получить формулы предельной ошибки для каждого вида отбора. Например, для повторного отбора предельная ошибка выборочной средней примет вид:
 (94)
(94)
Остальные виды предельных ошибок получают аналогично.
Предельная ошибка позволяет определить границы среднего значения признака в генеральной совокупности с заданной степенью вероятности. Например, если вероятность (надежность) ошибки репрезентативности должна быть 954 случая из 1000, значение коэффициента доверия t составит 2, т.е. предельная ошибка репрезентативности должна быть выше средней в 2 раза. Определить значение коэффициента доверия при любой степени вероятности можно на основе таблицы функции Лапласа. Выписка из таблицы функции Лапласа приведена в таблице 5.
Таблица 5- Выписка из таблицы функции Лапласа
| F(t) | t | F(t) | t | F(t) | t | F(t) | t |
| 0,663 | 0,96 | 0,911 | 1,70 | 0,932 | 1,83 | 0,947 | 1,94 |
| 0,676 | 0,99 | 0,920 | 1,75 | 0,937 | 1,86 | 0,954 | 2,00 |
| 0,854 | 1,46 | 0,929 | 1,81 | 0,942 | 1,92 | 0,997 | 3,00 |
При использовании предельной ошибки репрезентативности пределы генеральной средней и генеральной доли альтернативного признака определяются следующим образом:
 или
или  (95)
(95)
 или
или  (96)
(96)
В ходе выборочного наблюдения одним из вопросов является определение объема выборочной совокупности. Определить оптимальную численность можно, используя формулу предельной ошибки репрезентативности, следовательно, выбор формулы зависит от способа формирования выборочной совокупности. В таблице 6 приведены формулы для определения оптимальной численности выборки при каждом способе отбора для расчета выборочной средней и выборочной доли альтернативного признака.
Следует помнить, что расчет оптимальной численности возможен только в том случае, когда изначально известны величины дисперсии и предельной ошибки репрезентативности. Поэтому определять оптимальную численность рекомендуется только при проведении повторных выборочных наблюдений.
Таблица 6 - Формулы для расчета численности выборки
| Вид отбора и объем выборочной совокупности | Для выборочной средней | Для доли альтернативного признака | ||
| Формула | Номер формулы | Формула | Номер формулы | |
| Повторный отбор | 
| (97) | 
| (98) |
| Бесповторный отбор | 
| (99) | 
| (100) |
где nx, nw - оптимальная численность выборки;
t - коэффициент доверия;
 - дисперсия;
- дисперсия;
 - предельная ошибка выборки;
- предельная ошибка выборки;
 - предельная ошибка доли альтернативного признака;
- предельная ошибка доли альтернативного признака;
N – объем генеральной совокупности;
w - доля альтернативного признака в выборочной совокупности.