T-критерий для связанных (зависимых) измерений
Тема 10 Оценка достоверности различий при повторных измерениях
Задания для самостоятельной работы.
1. Определить достоверность различий между показателями среднего балла интеллекта у мальчиков и у девочек. Значения брать из Таблицы I Приложения. Использовать t-критерий Стьюдента.
2. Определить достоверность различий между показателями успеваемости у мальчиков и у девочек. Значения брать из Таблицы I Приложения. Использовать t-критерий Стьюдента.
3. Определить достоверность различий между показателями субтеста «арифметика» у мальчиков и у девочек. Значения брать из Таблицы I Приложения. Использовать U-критерий Манна-Уитни.
4. Определить достоверность различий между показателями субтеста «понятливость» у мальчиков и у девочек. Значения брать из Таблицы I Приложения. Использовать U-критерий Манна-Уитни.
С целью оценки достоверности сдвига значений в зависимых выборках используют t-критерий Стьюдента для зависимых измерений. Критерий для связанных выборок имеет следующую формулу:
,
где Мd – среднее арифметическое разностей индивидуальных значений, а σd - стандартное отклонение значений разностей. Количество степеней свободы df = n-1.
Следующий пример демонстрирует алгоритм расчета критерия. Перед началом первого учебного года был измерен уровень интеллекта у группы студентов. В начале второго учебного года при помощи параллельной методики вновь был измерен уровень интеллекта. Поскольку можно использовать результаты только одних и тех же людей, из дальнейшей обработки были исключены результаты тех студентов, которые оставили обучение в институте (которые не подверглись обследованию на фазе заключительных срезов). Можно ли сказать, что за год обучения интеллектуальный уровень студентов значимо изменился?
8. Формулируются статистические гипотезы.
Н0: сдвиг между показателями начальных и конечных срезов значимо не отличается от нуля.
Н1: сдвиг между показателями начальных и конечных срезов значимо отличается от нуля.
| n | Начальный срез (xi) | Конечный срез (yi) | di = yi - xi | di - Md | (di - Md)2 |
| 10,58 | 111,94 | ||||
| -4,42 | 19,54 | ||||
| 4,58 | 20,98 | ||||
| -2,42 | 5,86 | ||||
| 3,58 | 12,82 | ||||
| 3,58 | 12,82 | ||||
| -9 | -13,42 | 180,10 | |||
| 0,58 | 0,34 | ||||
| -1,42 | 2,02 | ||||
| 5,58 | 31,14 | ||||
| 1,58 | 2,50 | ||||
| -4 | -8,42 | 70,90 | |||
| n=12 | Σdi = 53 | Σ = 470,92 |
Мd = Σdi / n = 4,42
σd = 
= 6,54
tэмп =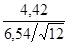 
= 2,341
df = 12 - 1 = 11
В нашем примере tкр при df = 11 составляет 2,201 при р ≤ 0,05. Таким образом,
tэмп > tкр (р ≤ 0,05) ¹> H0, Þ Н1! ст. зн.
То есть, мы можем принять на уровне статистической значимости гипотезу о достоверности сдвига значений интеллекта за год обучения.
Т-критерий Вилкоксона (ранговый критерий для повторных измерений)
Т-критерий Вилкоксона используется для решения тех же задач, что и t-критерий Стьюдента для связанных выборок. Отличие состоит в том, что Т-критерий Вилкоксона можно применять для порядковых данных, и исходные распределения не обязательно должны быть нормальными.
Формула имеет вид: Т = ΣRr. Где ΣRr – сумма нетипичных рангов.
Пояснить алгоритм расчета можно на следующем примере. Допустим, в кабине самолета (и на тренажере) изменили эргономическую среду. Для выполнения определенной задачи летчик раньше тратил одно количество секунд, а в новой среде он на выполнение тех же действий тратит другое количество времени. Таким образом, были сделаны замеры у 10 летчиков. Определить достоверность преобладания сдвига значений в направлении одной из сторон при условии, что результаты второго среза обусловлены исключительно изменением эргономической среды.
Формулируются статистические гипотезы.
Н0: преобладание сдвигов между начальными и конечными показателями в одном из направлений значимо не отличается от нуля.
Н1: преобладание сдвигов между начальными и конечными показателями в одном из направлений значимо отличается от нуля.
Определяются величины сдвигов между начальными и конечными показателями, затем они переводятся в абсолютные значения и ранжируются по принципу «меньшему значению – меньший ранг». Затем выделяются нетипичные (чья направленность отличается от большинства) ранги и подсчитывается их сумма.
| n | Начальные показатели | Конечные показатели | Разность показателей (d) | Абсолютное значение разности | Ранг разности |
| -5 | 4,5 | ||||
| 6,5 | |||||
| -6 | 6,5 | ||||
| 2,5 | |||||
| 2,5 | |||||
| -5 | 4,5 |
Следует обратить внимание: в нашем примере одно из значений d равно 0. Поэтому при ранжировании разностей мы присваиваем ему нулевой ранг.
В таблице нетипичные ранги выделены жирным шрифтом. Сумма нетипичных рангов равна искомому эмпирическому значению. Тэмп = 4,5+6,5+4,5=15,5
Для Т-критерия Вилкоксона правило принятия-отвержения нулевой гипотезы следующее: Тэмп ≤ Ткр Þ Н1!
Следует дополнительно добавить, что этот критерий может быть односторонним (если направление сдвигов предсказывается) и двусторонним (если мы не предсказываем направление сдвигов). Уровни значимости для одностороннего и двустороннего критерия различны.
В нашем случае мы имеем дело с двусторонним критерием, так как предварительно не предсказывали направление различий. Для n = 10 критическое значение при (р ≤ 0,05) составляет 10. То есть Тэмп > Ткр (р ≤ 0,05) Þ Н0! Мы можем констатировать, что достоверность преобладания сдвигов ни в одном из направлений не установлена. Возможно, что мы могли бы опровергнуть нулевую гипотезу, если бы увеличили количество наблюдений.