Экспоненциальный сигнал
Пусть задан сигнал вида (рисунок 10):
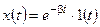 ,
,
где  - функция включения (функция Хевисайда, “ ступенька”) (рисунок 11).
- функция включения (функция Хевисайда, “ ступенька”) (рисунок 11).
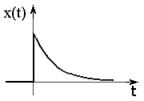

Рисунок 10 – Экспоненциальный импульс Рисунок 11 – Функция включения
Спектр экспоненциального импульса равен:
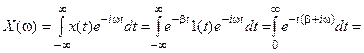
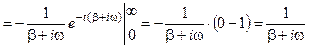 ,
,
то есть спектральная функция является величиной комплексной. Рассчитаем ее модуль:
 .
.
Обозначим  , тогда
, тогда  и
и  . Для построения графика спектра (рисунок 12) рассмотрим несколько частных случаев:
. Для построения графика спектра (рисунок 12) рассмотрим несколько частных случаев:
1) при  ;
;
2) при  ;
;
3) при  ;
;
4) при  , то есть модуль спектра безграничен.
, то есть модуль спектра безграничен.

Рисунок 12 – Модуль спектра экспоненциального импульса
Что принять за ширину спектра экспоненциального импульса? Нижняя граница спектра равна нулю, а в качестве верхней границы можно выбрать значение частоты, при которой модуль спектра уменьшится до 70% от начального значения  , то есть
, то есть  или до 45% при
или до 45% при  и т.д. Выбор граничного значения неоднозначен.
и т.д. Выбор граничного значения неоднозначен.
Аналогичные рассуждения справедливы и для определения длительности экспоненциального импульса, поскольку он начинается при t = 0 и уменьшается до нуля при t ® ¥. Можно принять за длительность промежуток времени, за который амплитуда импульса спадает до 5% от начального значения  , то есть Dt = 3T. Действительно:
, то есть Dt = 3T. Действительно:
 .
.
Длительность импульса Dt = 4T соответствует уменьшению амплитуды импульса до 2%.
Проследим за изменением произведения  при различном выборе длительности импульса и ширины спектра:
при различном выборе длительности импульса и ширины спектра:

 ;
;
 ,
,
то есть произведение  остается по порядку равным единице.
остается по порядку равным единице.
Ключ к пониманию проблемы о выборе длительности импульса и ширины его спектра дает соотношение, справедливое для интегрального преобразования Фурье и известное как теорема Рэйли. Оно аналогично неравенству Бесселя для рядов Фурье. Теорема утверждает равенство энергий во временной и частотной областях представления сигнала:
 , (7)
, (7)
где  ;
;
 - спектр сигнала
- спектр сигнала  ;
;
 - величина, комплексно–сопряженная к
- величина, комплексно–сопряженная к  .
.
Во временном представлении энергия распределена по времени, в частотном – по частоте, но, в принципе, она неизменна.
Упорядочить выбор для сигнала  и
и  позволяет использование понятий энергии и эффективной длительности (ширины).
позволяет использование понятий энергии и эффективной длительности (ширины).
Эффективная длительность импульса определяется промежутком времени, в котором сосредоточена подавляющая часть его энергии. Аналитически это выглядит следующим образом:

где h - относительная доля полной энергии, приходящейся на промежуток  .
.
Аналогично определяется и эффективная ширина спектра сигнала:
 .
.
В большинстве случаев просчитать эффективные характеристики сигнала возможно только численными методами.
Харкевич А.А. в своих работах приводит вычисленные произведения  , которые определены при
, которые определены при  (за длительность импульса принимается временной промежуток, в котором содержится 90% полной энергии; за ширину спектра – частотный промежуток, в котором содержится 90% полной энергии):
(за длительность импульса принимается временной промежуток, в котором содержится 90% полной энергии; за ширину спектра – частотный промежуток, в котором содержится 90% полной энергии):
- для прямоугольного импульса  ;
;
- для экспоненциального импульса  ;
;
- для треугольного импульса  .
.
Общий вывод (принцип неопределенности для сигнала): произведение эффективной длительности сигнала на эффективную ширину его спектра есть величина постоянная, по порядку равная единице  .
.
Иными словами, чем короче импульс, тем шире его спектр и наоборот. Это соблюдается для всех форм сигнала.
Принцип неопределенности был открыт Гейзенбергом в квантовой механике и относился к точности одновременного определения координаты  и импульса
и импульса  электрона. Он гласит, что их произведение неизменно и равно постоянной Планка h:
электрона. Он гласит, что их произведение неизменно и равно постоянной Планка h:
 .
.
Это правило оказалось справедливым и для представления сигналов во временной и частотной формах, что крайне важно с практической точки для импульсной техники. Нельзя создать короткий импульс с очень узким спектром. Произведение  обязательно больше некоторой константы, близкой по значению к единице.
обязательно больше некоторой константы, близкой по значению к единице.