Определение дирекционных углов и румбов сторон полигона
Для определения дирекционного угла каждой из сторон теодолитного хода необходимо знать исходный дирекционный угол одной из сторон. Этот угол получают путем привязки данной стороны к пункту геодезической опорной сети или определением для этой стороны истинного или магнитного азимута. По известному дирекционному углу и по откорректированным после расчетов невязок значениям углов полигона вычисляют дирекционные углы всех сторон по формулам:
α2 = α1 + 180О – β2;
α3 = α2 + 180О – β3;
α4 = α3 + 180О – β4;
αn = αn-1 + 180О – βn;
α1 = αn + 180О – β1;
Последняя строка в системе равенств – контрольная. Она как бы замыкает выполненные расчеты и показывает, что в замкнутом полигоне сумма измеренных и рассчитанных углов удовлетворяет соответствующим условиям.
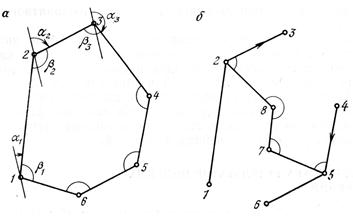 Рис . Схема обработки теодолитных ходов.
Рис . Схема обработки теодолитных ходов.
а – замкнутого; б – диагонального.
Прямая и обратная задача геодезии
Прямая задача: даны координаты X1 и Y1 точки А начала линии АВ и дирекционный угол α. Требуется определить координаты X2 и Y2 точки В.
Из рисунка следует, что координаты точки В конца линии АВ:
X2 = X1 + ΔX;
Y2 = Y1 + ΔY;,
Где ΔX; и ΔY есть приращения координат. Очевидно, что:
ΔX = d · cos α
ΔY = d · sin α
При помощи румбов приращения координат можно вычислить как: ΔX = ± d · cos(r) ; ΔY = ± d · sin(r) – в зависимости от дирекционного угла или названия румба. . При этом приращения координат имеют соответствующий знак + и.
Обратная задача геодезии: даны координаты X1 и Y1 точки А начала линии АВ и координаты X2 и Y2 точки В – конца этой линии. Требуется определить дирекционный угол и длину этой линии.
Из рисунка следует, что:
tg α = (Y2 - Y1)/(X2 – X1);
d = √ (ΔX2 + ΔY2);
или d = ΔX / cos r = ΔY / sin r;
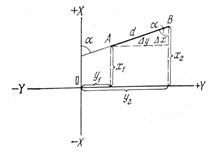 |
Рис. . Прямая и обратная геодезическая задачи
Вычисление координат вершин теодолитного хода. Невязки в приращениях координат замкнутого полигона вычисляются, исходя из факта равенства нулю суммы проекций полигона на координатную ось. То есть: ΣΔX = 0 и ΣΔY = 0. Вследствие ошибок измерений фактическая сумма приращений координат нулю оказывается не равной.
Тогда ΣΔX = fx и ΣΔY = fy называются, соответственно, невязками в приращениях координат по оси абсцисс и оси ординат. Перед распределением невязок по координатам необходимо определить их допустимость по формуле:
fp / P ≤ 1 / 2000,
где невязка в периметре fp = 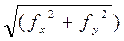 , а Р – периметр полигона. Если невязка допустима, то невязки fx и fy распределяются с обратным знаком на каждое приращение ΔX и ΔY пропорционально длинам линий с округлением их до 0,01 м. Контролируют вычисления поправок в приращениях координат по ранее вычисленной сумме. Сумма исправленных приращений по каждой оси в замкнутом полигоне должна равняться 0.
, а Р – периметр полигона. Если невязка допустима, то невязки fx и fy распределяются с обратным знаком на каждое приращение ΔX и ΔY пропорционально длинам линий с округлением их до 0,01 м. Контролируют вычисления поправок в приращениях координат по ранее вычисленной сумме. Сумма исправленных приращений по каждой оси в замкнутом полигоне должна равняться 0.
После исправления приращений координат определяют координаты всех вершин полигона по исходной координате первой точки, привязанной к опорной геодезической сети. Контролем вычисления координат является последовательное вычисление координат точек замкнутого полигона, чтобы в результате получить координаты исходной точки.
Таблица: Ведомость вычисления координат основного полигона
| № вершин хода | Углы β | Дирекционные углы | Румбы | Длина линий, м | Приращения координат | Координаты | № вершин хода | ||||||||||||||||
| вычисленные | исправленные | ||||||||||||||||||||||
| Измеренные | Исправленные | град | мин | град | мин | ± | ΔX | ± | ΔY | ± | ΔX | ± | ΔY | ± | X | ± | Y | ||||||
| +0,2 | |||||||||||||||||||||||
| 10,5 | 10,7 | +0,10 | -0,02 | + | 500,00 | + | 500.00 | ||||||||||||||||
| +0,2 | 40,0 | СВ | 40,0 | 335,29 | + | 329,50 | + | 62,06 | + | 329,60 | + | 62,04 | |||||||||||
| 03,0 | 03,2 | +0,05 | -0,01 | + | 829,60 | + | 562,04 | ||||||||||||||||
| +0,2 | 36,8 | СВ | 36,8 | 177,79 | + | 53,13 | + | 169,67 | + | 53,18 | + | 169,66 | |||||||||||
| 32,0 | 32,2 | +0,08 | -0,01 | + | 882,78 | + | 731,70 | ||||||||||||||||
| +0,2 | 04,6 | ЮВ | 55,4 | 257,28 | - | 220,71 | + | 132,21 | - | 220,63 | + | 132,20 | |||||||||||
| 22,0 | 22,2 | +0,05 | -0,01 | + | 662,15 | + | 863,90 | ||||||||||||||||
| +0,2 | 42,4 | ЮЗ | 42,4 | 185,82 | - | 167,43 | - | 80,60 | - | 167,38 | - | 80,61 | |||||||||||
| 01,5 | 01,7 | +0,05 | + | 494,77 | + | 783,29 | |||||||||||||||||
| +0,2 | 40,7 | ЮЗ | 40,7 | 166,58 | - | 44,02 | - | 160,66 | - | 43,97 | - | 160,66 | |||||||||||
| 49,8 | 50,0 | +0,04 | + | 450,80 | + | 622,63 | |||||||||||||||||
| 50,7 | СЗ | 09,3 | 132,12 | + | 49,16 | - | 122,63 | + | 49,20 | - | 122,63 | ||||||||||||
| -0,37 | +0,05 | 500,00 | 500,00 | ||||||||||||||||||||
| Σβn | 58,8 | 00,0 | |||||||||||||||||||||
| Σβt | 00,0 | 00,0 | |||||||||||||||||||||
| fβ | - | 01,2 | 00,0 | ||||||||||||||||||||
| fдоп | ± | 02,4 |
Σβт = 180 (n – 2);