ФОРМУЛА И Многочлен Тейлора

РАЗДЕЛ. Основные теоремы о дифференцируемых функциях

Инвариантность формы первого дифференциала и неинвариантность формы высших дифференциалов функции

Пусть . Тогда т.е.

 

и .

Здесь – независимая переменная, а g – функция зависящая от х.

И, тем не менее, формулы для нахождения первого дифференциала одинаковы.

Это явление выражает инвариантность формы первого дифференциала относительно замены переменных.

 

Теперь для независимой переменной х:

=

= .

А для зависимой переменной g :

.

Получили:

, если х – независимая переменная, и

, если g – зависимая переменная т.е. функция.

Это и есть не инвариантность формы второго (и, естественно, более высоких) дифференциала относительно замены переменных.

 

Функция называется возрастающей в некоторой окрестности точки , если

.

Функция называется убывающей в некоторой окрестности точки , если

.

Если функция дифференцируема в точке и ее производная больше (меньше) нуля, то она возрастает (убывает) в этой точке.

т.е.

- а это и есть возрастание функции, имеющей положительную производную.

Аналогично для убывания функции, имеющей отрицательную производную.

 

Пусть .

Если для значений M и m справедливо, что

и ,

то говорят, что достигаются максимальное и минимальное значения функции, и они обозначаются: .

 

Пусть . Тогда:

• Если это справедливо на всей области определения функции 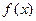, то говорят, что это глобальный максимум и глобальный минимум.
• Если это справедливо на некотором подмножестве - мы имеет место локальный максимум и локальный минимум.
• Строгий максимум, если
  не строгий максимум, если
  аналогично определяются строгий минимум и нестрогий минимум.
• Точки максимума и минимума называются точками экстремума.
• Внутренний экстремум – достигается внутри .
• Краевой экстремум – в граничной точке .

 

Т°(Ферма).В точке локального внутреннего экстремума производная функции, если она существует и конечна, равна нулю.

 

∆(для max). Пусть функция 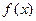в точке имеет локальный внутренний максимум.

Тогда : .

Получаем :

и Þ . ▲

 

Т°(Ролля).Если функция 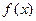дифференцируема внутри замкнутого промежутка и непрерывна на нем, причем на концах промежутка, принимает равные значения, то внутри промежутка найдется точка с нулевой производной (хотя бы одна).

.

∆. Функция непрерывная на замкнутом промежутке необходимо ограничена на нем т.е.

причем m, M – достигаются. Возможны два случая:

a) .

b) существует хотя бы один внутренний локальный экстремум.

Следовательно, по теореме Ферма, . ▲

 

Т° (Лангранжа).Если функция непрерывна на замкнутом промежутке и дифференцируема внутри него то внутри промежутка есть точка, в которой касательная параллельна хорде, соединяющей точки и .

 

∆ Рассмотрим , где L некоторая постоянная.

По условию теоремы - непрерывна на [a,b], дифференцируема на (a,b) .

Константу L подберем из условия : F(a) = F(b).

Получим:

f (a) + La = f (b) + Lb, f (a) – f (b) = L(b-a) .

Так построенная функция удовлетворяет условиям теоремы Ролля . Значит

т.е. . ▲

 

 

Следствие: Если 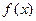на дифференцируема, то

Þ

Þ Þ

Þ

Полученная формула называется формулой конечных приращений.

 

Tº (Формула Коши). Если две функции непрерывны на замкнутом промежутке дифференцируемы внутри него и:

· их производные одновременно не равны 0;

· значения одной из функций на концах промежутка не совпадают;

то внутри промежутка есть точка где касательная к кривой, заданной параметрическими уравнениями, определяемыми этими функциями параллельна хорде.

Ù f´²(t) + g´²(t) ≠ 0 Ù ( f(a) ≠ f(b) g(a) g(f) )

Þ $aÎ(a, b) .

∆ Пусть g(a) g(b) .

Рассмотрим функцию : F(x) = f (x) – Lg(x) . Эта функция F(x) = f (x) – Lg(x) непрерывна на [a,b] и дифференцируема на (a,b).

Потребуем: F(а) = F(b) Þ f (а) – Lg(а) = f (b) – Lg(b) . Тогда L= и по теореме Ролля : Þ при t = Þ

Þ Þ . ▲

Tº (Дарбу). Произвольная функция, дифференцируемая на замкнутом промежутке, и принимающая два некоторых значения принимает и всякое промежуточное значение.

· Частный случай : Если на концах промежутка функция имеет производную разных знаков, то внутри промежутка есть точка, в которой производная равна нулю.

∆ Пусть и γ (, β).

Рассмотрим функцию F(x) = f (x) – γx.

Для неё : ;

.

на концах промежутка принимает значения разных знаков, следовательно

. ▲

 

Tº (Об односторонней производной).Если функция f определена в односторонней окрестности точки x = a и непрерывна в ней , а в соответствующей проколотой окрестности дифференцируема, то односторонняя производная равна соответствующему пределу производной в этой точки: .

∆ Пусть . Тогда .

Т.к. a < γ(x) < x , то .

Если в формуле: устремить x → a + 0, то получим

. ▲

 

 

Пусть f (x) – n-кратно дифференцируема в т. х₀. Полиномом Тейлора этой функции называется

.

Все производные P_n (f, x₀; x) от нулевой до n-ной совпадают с соответствующей функцией f (x). Разность между функцией f (x) и ее полиномом Тейлора называется остаточным членом формулы Тейлора

R_n (f, x₀; x) º f (x) – P_n (f, x₀; x) ,

А представление f (x) º P_n (f, x₀ (f, x₀; x) ,

А представление f (x) º P_n (f, x₀; x) + R_n (f, x₀; x) называется формулой Тейлора для функции f (x) в окрестности точки x₀. При этом все производные остаточного члена

R_n (f, x₀; x) от нулевой до n-ной равны 0 в т. х₀.