Разрывы монотонной функции.
Классификация точек разрыва
Условие непрерывности функции f (x) в т.  :
:
 .
.
При нарушении этого условия в т.  , функция f (x) имеет разрыв.
, функция f (x) имеет разрыв.
Разрывы бывают:
Разрывы 1-го рода (когда пределы справа и слева функции f (x) в т.  существуют и конечны).
существуют и конечны).
1°. 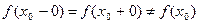 устранимый разрыв первого рода.
устранимый разрыв первого рода.
2°. 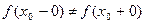 разрыв первого рода типа скачок.
разрыв первого рода типа скачок.
Разрывы 2-го рода (по крайней мере, один из односторонних пределов равен ∞ или не существует).
1°. 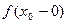 или
или 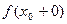 равен ∞ бесконечный разрыв 2-го рода.
равен ∞ бесконечный разрыв 2-го рода.
1°. 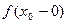 или
или 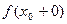 не существует разрыв 2-го рода.
не существует разрыв 2-го рода.
Примеры:
1°. y = sgn x при x = 0разрыв 1-го рода типа скачок
величина скачка: 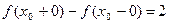 .
.
2°. y = |sgn x| при x = 0устранимый разрыв 1-го рода.
3°.  при x = 0устранимый разрыв 1-го рода.
при x = 0устранимый разрыв 1-го рода.
4°.  наибольшее целое на превосходящее х – целая часть х.
наибольшее целое на превосходящее х – целая часть х.
В целочисленных точках – непрерывность справа, разрывы 1-го рода типа скачок слева.
5°.  разрыв 2-го рода в т. х = 0.
разрыв 2-го рода в т. х = 0.
6°.  при x = 0устранимый разрыв 1-го рода.
при x = 0устранимый разрыв 1-го рода.
7°. 
 функция непрерывна.
функция непрерывна.
8°.  при x = 0бесконечный разрыв 2-го рода.
при x = 0бесконечный разрыв 2-го рода.
9°. y = arctg при x = 0разрыв 1-го рода типа скачок.
при x = 0разрыв 1-го рода типа скачок.
10°. Функция Дирихле: y = D(x) =  разрывна в любой точке.
разрывна в любой точке.
11°. y = xD(x) непрерывна только в одной точке х = 0.
Т˚. Монотонно возрастающая (убывающая) на промежутке Х функция f (x) может иметь во внутренних точках лишь разрывы 1-го рода.
∆ Пусть  - внутренняя точка Х и f (x) монотонно возрастает. Тогда слева от
- внутренняя точка Х и f (x) монотонно возрастает. Тогда слева от 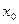
f (x) < f (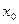 ) и, следовательно, ограничена сверху.
) и, следовательно, ограничена сверху.  и:
и:
а) если  то функция непрерывна слева в т.
то функция непрерывна слева в т. ,
,
б) если  то функция разрывна слева в т.
то функция разрывна слева в т. .
.
Тогда справа от 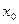 функция f (x) > f (
функция f (x) > f (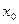 ) и, следовательно, ограничена снизу. Следовательно ,
) и, следовательно, ограничена снизу. Следовательно ,  и:
и:
а) если  то функция непрерывна справа в т.
то функция непрерывна справа в т. ,
,
б) если  то функция разрывна справа в т.
то функция разрывна справа в т. .
.
Т.к. пределы функции в точке и слева и справа существуют и конечны, то в т. , в худшем случае, будут разрывы 1-го рода.
, в худшем случае, будут разрывы 1-го рода. ▲
▲
Т˚. (Критерий непрерывности монотонной функции). Если значения монотонно возрастающей функции содержатся в промежутке Y и сплошь заполняют его (т.е.  ), то эта функция непрерывна на Х. ∆▲
), то эта функция непрерывна на Х. ∆▲
§ Теорема о промежуточном значении непрерывной функции (Больцано-Коши)
Т˚. Функция, непрерывная на промежутке и принимающая какие-либо два значения, принимает и всякое промежуточное значение. (Значения, которые принимает непрерывная функция на промежутке, сами заполняют некоторый промежуток).
Пусть I – интервал;  . f (a) = α; f (b) = β.
. f (a) = α; f (b) = β.
Тогда 
 | f (c) = γ.
| f (c) = γ.
Вспомогательный факт: если f (x) непрерывна в т. 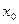 и f (
и f (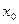 ) = ξ > γ,
) = ξ > γ,
то 
 f (x) > γ.
f (x) > γ.
Аналогично: если f (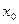 ) = ξ < γ
) = ξ < γ
то 
 f (x) < γ.
f (x) < γ.
∆ Рассмотрим все  , для которых
, для которых  . Т.е.
. Т.е. 
 .
.
Множество Х – не пусто, т.к. f (a)< γ и ограничено сверху (например, числом b).
Тогда  .
.
Докажем, что f (c) = γ (от противного).
1). 

 , т.е.
, т.е. 
 ,
,
что противоречит тому, что с = sup X.
2). 

 , т.е.
, т.е. 
 ,
,
и это вновь противоречит тому, что с = sup X.
Таким образом f (c) = γ. ▲
Т˚. Непрерывная на замкнутом промежутке  функция f (x), на концах промежутка принимающая значение разных знаков, неминуемо внутри промежутка обращается в ноль.
функция f (x), на концах промежутка принимающая значение разных знаков, неминуемо внутри промежутка обращается в ноль.
∆ Доказательство проведем методом вилок :
Положим  и
и  . Делим отрезок
. Делим отрезок  пополам точкой с . Если
пополам точкой с . Если  то теорема доказана. Если же
то теорема доказана. Если же  , то на одном из двух промежутков
, то на одном из двух промежутков  или
или  функция имеет разные знаки на концах . Пусть это отрезок, например
функция имеет разные знаки на концах . Пусть это отрезок, например  .
.
Положим  и
и  . Получим промежуток
. Получим промежуток  .
.
Продолжая эту процедуру мы либо на некотором конечном шаге найдем точку с в которой  , либо получим бесконечную последовательность вложенных замкнутых промежутков, удовлетворяющих условию
, либо получим бесконечную последовательность вложенных замкнутых промежутков, удовлетворяющих условию  .
.

При этом:  . Значит существует с - общая точка всех промежутков для которой справедливы равенства :
. Значит существует с - общая точка всех промежутков для которой справедливы равенства : . Учитывая что,
. Учитывая что,  делаем заключение :
делаем заключение :  . ▲
. ▲
§ Существование экстремумов непрерывной функции на сегменте (теорема Вейерштрасса)
Т˚ Функция непрерывная на замкнутом промежутке необходимо ограничена на этом промежутке и достигает на нём своих точных верхней и нижней граней.

 |
|  |
| 
∆ 1)  Допустим, что f (x) неограниченна сверху для
Допустим, что f (x) неограниченна сверху для  . Тогда
. Тогда  |
| 
Построив последовательность  выделим из неё сходящуюся последовательность
выделим из неё сходящуюся последовательность  , тогда, по непрерывности
, тогда, по непрерывности  , но
, но  . Полученное противоречие, доказывает ограниченность функции сверху. (Аналогично доказывается ограниченность функции снизу.
. Полученное противоречие, доказывает ограниченность функции сверху. (Аналогично доказывается ограниченность функции снизу.
2) Докажем, что  достигается, т.е.
достигается, т.е.  |
|  .
.
Вновь от противного: пусть это не так. Тогда 

Рассмотрим  непрерывна и, следовательно (из 1)), ограничена, т.е.
непрерывна и, следовательно (из 1)), ограничена, т.е.  , т.е.
, т.е.  .
.
Последнее неравенство противоречит тому, что  . (аналогично с точной нижней гранью). ▲
. (аналогично с точной нижней гранью). ▲
Т°. (об обратной функции). Если y = f (x) определена, монотонно возрастает (убывает) и непрерывна в некотором промежутке Х, то в соответствующем промежутке Y значений этой функции существует однозначная обратная функция x =  также монотонно возрастающая (убывающая) и непрерывная.
также монотонно возрастающая (убывающая) и непрерывная.
∆ (для возрастающей функции) . Отметим, что 
1) Существование обратной функции. Если f (x) непрерывна, то её значения заполняют промежуток Y сплошным образом, т.е.  |
|  . Единственность такого x следует из монотонности исходной функции.
. Единственность такого x следует из монотонности исходной функции.
Тогда :  , т.е. x =
, т.е. x =  .
.
2) Монотонность. Пусть  . Т.е. x =
. Т.е. x =  – монотонна.
– монотонна.
3) Непрерывность (из критерия непрерывности монотонной функции). Значения
x =  сплошь заполняют промежуток Х и
сплошь заполняют промежуток Х и  – монотонна. ▲
– монотонна. ▲