Примеры.

Множество называется неограниченным если оно неограничено сверху или снизу.

Множество называется ограниченным, если оно ограничено сверху и ограничено снизу.

Любое число меньшее нижней грани, естественно, также является нижней гранью.

Любое число большее верхней грани, естественно, также является верхней гранью.

При этом L называется верхней, а l нижней гранями множества X.

ГРАНИ ЧИСЛОВЫХ МНОЖЕСТВ

РАЗДЕЛ 2. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ

Пример: Множество вещественных чисел R является множеством мощности континиум.

Def: Множества, равномощные множеству точек, принадлежащих интервалу (0, 1) называются множествами мощности континиум.

 

Одной из проблем, возникших в теории множеств и долгое время ожидавших своего решения, являлась так называемая проблема ²континиума²: существуют ли множества с мощностью большей мощности счетного множества, но меньшей мощности континиума?

Проблема была решена американским математиком Полем Коэном. Он доказал, что существование или отсутствие таких множеств не вытекает из аксиом теории множеств и может быть принято в качестве еще одной аксиомы теории множеств.

 

 

1^○Множество X называетсяограниченным сверху (снизу)если существует вещественное L ( l ) число такое, что L больше ( l меньше) любого элемета X.

Ограниченное сверху: $LÎR "x ÎX x £ L.

Ограниченное снизу: $l Î R "x ÎX x ³ l.

$L , l Î R "x ÎX l £ x £ L или, что то же самое, $А Î R "x ÎX | x | < А .

 

2^○Множество X называетсянеограниченным сверху, если "LÎR $x ÎX x >L. Множество X называетсянеограниченным снизу, если : "l Î R $x ÎX x < l.

 

3^○Наименьшая из верхних граней множества, если она существует, называется точной верхней гранью L* множества X и обозначается : L* = sup X

L* : 1. "x ÎX x £ L* 2. "e>0 $x ÎX x > L* -e.

Наибольшая из нижних граней множества, если она существует, называется точной нижней гранью l* множества X и обозначается : l* = inf X

l* : 1. "x ÎX x > l* 2. "e>0 $x ÎX x < l* -e.

 

4^○Если L* ÎX , то L* называется максимальным элементом множества X.

L* = sup X = max X.

Аналогично, если l* ÎX , то l* называется минимальным элементом множества X.

l* = inf X = min X.

Из этих определений ясно, что максимальный элемент множества X одновременно является и точной верхней гранью множества а минимальный элемент множества X одновременно является и точной нижней гранью множества. Обратное, вообще говоря, неверно.

 

1^○ X= [ a, b]. a = inf X = minX, b = supX = maxX.

2^○ X= ( a, b). a = inf X , b = supX . Наибольшего и наименьшего элементов интервала не существует.

 

Т^○Еслинепустое числовоемножество ограничено сверху (снизу), то оно имеет точную верхнюю (нижнюю) грань. ∆ ▲

 

·
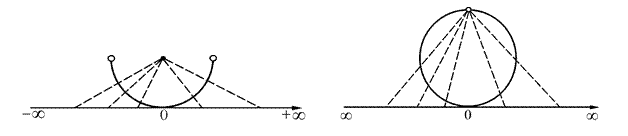
Числовую прямую R можно расширить.

 

Рисунки иллюстрируют тот факт, что числовая прямая R, расширенная +¥ и -¥ топологически эквивалентна полуокружности с включенными крайними точками дуги или отрезку, а числовая прямая R, расширенная ¥ топологически эквивалентна окружности.

 

Т^○Начисловой прямой R, расширенной +¥ и -¥ всякое непустое числовоемножество имеет точную верхнюю и точную нижнюю грань (может быть несобственную). ∆ ▲