АНАЛИТИЧЕСКИЙ МЕТОД
При аналитическом доказательстве теоремы  x
x  M: A(x)
M: A(x)  В(х) цепочка силлогизмов строится так, что мысль движется от заключения теоремы к ее условию. Различают два вида аналитического метода: восходящий анализ (анализ Паппа), нисходящий анализ (анализ Евклида).
В(х) цепочка силлогизмов строится так, что мысль движется от заключения теоремы к ее условию. Различают два вида аналитического метода: восходящий анализ (анализ Паппа), нисходящий анализ (анализ Евклида).
Восходящим анализом (совершенным анализом) называется такая разновидность аналитического метода, при которой, отталкиваясь от заключения, подбирают для него достаточное условие — такое суждение 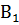 (х), что
(х), что 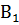 (х) ⇒ В(х), затем подбирают достаточное условие
(х) ⇒ В(х), затем подбирают достаточное условие  (х) для
(х) для 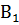 (х), такое, чтобы
(х), такое, чтобы  (х) ⇒
(х) ⇒ 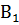 (х) было истинным, и так далее до тех пор, пока не получат такое достаточное условие
(х) было истинным, и так далее до тех пор, пока не получат такое достаточное условие  (х) для
(х) для  (х), что
(х), что  (х) ⇒
(х) ⇒  (х) и
(х) и  (х) выполняется (истинно). При этом используется как условие А(х) доказываемого предложения, так и некоторая совокупность Т связанных с А(х) и В(х) предложений данной теории, истинность которых уже была установлена.
(х) выполняется (истинно). При этом используется как условие А(х) доказываемого предложения, так и некоторая совокупность Т связанных с А(х) и В(х) предложений данной теории, истинность которых уже была установлена.
Сущность метода восходящего анализа состоит в том, что рассуждения строятся по схеме: для того чтобы В(х) было верно, достаточно, чтобы было верно С(х), и т. д.
Рассмотрим доказательство теоремы методом восходящего анализа.
Теорема: «Диагонали ромба взаимно перпендикулярны».
Доказательство
1) Для того чтобы доказать, что AC ⊥ BD (рис. 21), достаточно доказать, что ВО ⊥ АС.
2) Для того чтобы доказать, что ВО  АС, достаточно доказать, что ВО — высота треугольника ABC.
АС, достаточно доказать, что ВО — высота треугольника ABC.
3) Для того чтобы доказать, что ВО является высотой треугольника ABC, достаточно доказать, что треугольник ABC равнобедренный и ВО в нем является медианой.
4) Для того чтобы доказать, что треугольник ABC равнобедренный, достаточно доказать, что в нем АВ = ВС.
5) Но АВ = ВС по условию (ABCD — ромб) и ВО — медиана треугольника ABC (так как АО = ОС по свойству диагоналей параллелограмма).

Рис. 21
Теперь, идя обратным путем, от пункта 5 к пункту 1, мы и докажем сформулированную теорему.
Нисходящим анализом (несовершенным анализом) называют такую разновидность аналитического метода, при которой, отталкиваясь от заключения В(х) доказываемого предложения А(х) ⇒ В(х), рассуждения ведут путем последовательного получения логических следствий: В(х) ⇒ 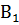 (х) ⇒
(х) ⇒  (х) ⇒
(х) ⇒  (х) ⇒
(х) ⇒  (х), где
(х), где  (х) есть предложение, истинное значение которого нам точно известно. При выведении следствий из В(х) временно допускают, что оно истинно.
(х) есть предложение, истинное значение которого нам точно известно. При выведении следствий из В(х) временно допускают, что оно истинно.
При нисходящем анализе, так же как и при восходящем, рассуждения ведут от заключения теоремы, но подбирают уже не достаточные, а необходимые условия.
При использовании нисходящего анализа возможны два основных случая.
Следствие  (х), полученное из В(х), истинно. В этом случае об истинности доказываемого предложения А(х) ⇒ В(х) ничего нельзя сказать, так как из ложного предложения может следовать и истинное.
(х), полученное из В(х), истинно. В этом случае об истинности доказываемого предложения А(х) ⇒ В(х) ничего нельзя сказать, так как из ложного предложения может следовать и истинное.
Например, из ложного предложения (а  b = b
b = b  а, а
а, а  b) следует истинное предложение (
b) следует истинное предложение ( 

 ).
).
Но в том случае, когда применение нисходящего анализа к доказательству теоремы  x
x  M: A(x)
M: A(x)  В(х) приводит к следствию
В(х) приводит к следствию  (х), которое истинно, целесообразно попытаться обратить этот аналитический процесс рассуждений в синтетическое доказательство:
(х), которое истинно, целесообразно попытаться обратить этот аналитический процесс рассуждений в синтетическое доказательство:
(  (х) ∧ А(х))
(х) ∧ А(х))  (х)
(х)  …
… 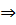
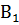 (х)
(х) 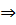 В(х).
В(х).
В таком случае нисходящий анализ позволит нам отыскать путь синтетического доказательства.
Для примера рассмотрим доказательство теоремы: D л
«Если в четырехугольнике противоположные стороны попарно равны, то четырехугольник — параллелограмм».
Доказательство
1) Пусть ABCD — параллелограмм (рис. 22). (В(х))
2) Тогда ВС || AD и АВ || DC. ( 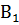 (х))
(х))
3) Тогда ∠ACB=∠CAD, ∠BAC = ∠ACD (как накрест лежащие углы при параллельных прямых и секущей). (  (х))
(х))
4) Из равенства этих углов с учетом того, что АС — общая сторона треугольников ABC и ADC, следует: ∆ABC = ∆ADC. (  (х))
(х))
5) Тогда AD = BC, AB = DC, АС=АС. (А(х))
Итак, имеем В(х)  (х)
(х)  (х)
(х)  (х)
(х) 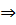 А(х), где А(х) — истинно.
А(х), где А(х) — истинно.
Проведя теперь рассуждения в обратном порядке А(х)  (х)
(х)  (х)
(х)  (х)
(х)  В(х), мы получим синтетическое доказательство.
В(х), мы получим синтетическое доказательство.
Следствие  (х), полученное из В(х), ложно, тогда всегда ложно и само В(х).
(х), полученное из В(х), ложно, тогда всегда ложно и само В(х).
Этот случай нисходящего анализа используется и для доказательства от противного. Так, чтобы доказать истинность предложения А(х) 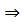 В(х), преобразуют его в предложение А(х)
В(х), преобразуют его в предложение А(х)  и к доказательству последнего применяют метод нисходящего анализа. Если следствие
и к доказательству последнего применяют метод нисходящего анализа. Если следствие  (х) окажется ложным, то этим будет доказана ложность предложения А(х)
(х) окажется ложным, то этим будет доказана ложность предложения А(х)  , а это, в свою очередь, доказывает истинность A(x)
, а это, в свою очередь, доказывает истинность A(x)  В(х).
В(х).

Рис. 22
Рассмотрим примеры доказательств методом нисходящего анализа (в данном случае мы используем метод доказательства от противного).
Теорема: «Разносторонний треугольник нельзя разбить на два равных треугольника».
Доказательство
1) Пусть ∆АВМ = ∆ВМС (рис. 23), АВ  ВС
ВС  АС.
АС.
2) В этих равных треугольниках ВМ — общая сторона и по теореме о том, что в равных треугольниках против равных сторон лежат равные углы, заключаем, что ∠ВАМ = ∠ВСМ.
3) По теореме о том, что если углы при основании треугольника равны, то треугольник равнобедренный, заключаем, что АВ = ВС.
4) Мы получили, что АВ = ВС, но по условию теоремы АВ  ВС. Получили противоречие.
ВС. Получили противоречие.
5) Значит, наше предположение неверно, а верно то, что
∆АВМ  ∆ВМС.
∆ВМС.
 C
C
Рис. 23
Рассмотрим пример из алгебры: «Доказать, что при любых а и b, отличных от нуля, хотя бы одно из уравнений 1992a  + 2x + 1993b = 0,
+ 2x + 1993b = 0,  x -
x -  = 0 имеет корень».
= 0 имеет корень».
Доказательство
Допустим, что оба уравнения не имеют корней. Тогда их дискриминанты должны быть отрицательны, т. е.
 = 4 – 4
= 4 – 4  1993
1993  1992
1992  ab
ab  0,
0,
 = 1 + 4
= 1 + 4 

 0.
0.
Но из (1) следует, что произведение аb положительно, а из
(2) следует, что произведение аb отрицательно.
Противоречие доказывает наличие корня хотя бы у одного заданного уравнения при указанных условиях.
Метод доказательства от противного более точно было бы называть «доказательство противоречием» (в методической ли- тературе этот метод еще называют методом приведения к абсурду). Доказательство противоречием строится на основе конструкции противоречия, к которой затем применяется синтетический метод.