Методика расчета крутого восхождения
Поиск оптимального значения функции отклика методом крутого восхождения включает следующие операции.
1. Проводится полный или дробный факторный эксперимент с центром в точке ( ).
).
2. Выполняется статистический анализ полученных данных и, в частности, вычисляются оценки параметров, т.е. коэффициенты регрессии bi, i=1,2,…,k которые являются составляющими вектор-градиента.
3. Выбирается несколько значений параметра λ , определяющего положение точек на линии крутого восхождения. Выбор таких значений осуществляется следующим образом:
1. Вычисляется произведение biYi .
2. Определяется базовый фактор, для которого произведение biYi является наибольшим по абсолютной величине.
3. Выбирается значение параметра λ=λ1 для первого шага в направлении крутого восхождения. Это значение выбирается таким образом, чтобы величина  , т.е. сдвиг по базовому фактору от основного уровня, у была равна интервалу варьирования Iв по этому фактору или части этого интервала т.е.
, т.е. сдвиг по базовому фактору от основного уровня, у была равна интервалу варьирования Iв по этому фактору или части этого интервала т.е.  .
.
Это условие выражается соотношением
 (6.18)
(6.18)
Отсюда
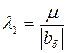 (6.19)
(6.19)
4. Вычисляются шаги и координаты первой точки крутого восхождения. В соответствии с выражениями (6.17) и (6.19) они находятся по уравнениям
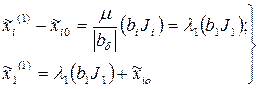 (6.20)
(6.20)
При необходимости численные значения величин  округляются.
округляются.
Находятся шаги и координаты последующих точек на этой линии:
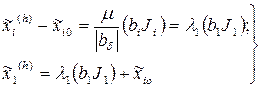 (6.21)
(6.21)
где h = 1,2,3,4,... - номер шага в направлении крутого восхождения.
Из всех реализованных опытов выбирается тот, который дал наилучшие результаты.
Выбор шага движения по градиенту относится к этапам планирования эксперимента, которые не формализованы. Небольшой шаг потребует значительного числа опытов при движении к оптимуму, а большой шаг увеличивает вероятность проскакивания области оптимума. Движение по градиенту наиболее эффективно при симметричной функции регрессии (когда величины коэффициентов различаются несущественно, меньше, чем на порядок). Удачным выбором интервалов варьирования можно сделать симметричной любую линейную функцию для значимых факторов. Методику расчета крутого восхождения рассмотрим на примере из области обработки металлов резанием [8].
Пример 6.7. Для повышения стойкости центровочных сверл решено оптимизировать значение факторов; угол при вершине 2φ, задний угол α , толщину сердцевины k. Критерием оптимизации служит показатель стойкости - количество просверленных отверстий. Испытания проводились до момента поломки сверла. На основе априорных данных выбраны основные уровни факторов, интервалы варьировании и реализован план эксперимента 2³ . Для оптимизации параметров сверл используем крутое восхождение,
. Для оптимизации параметров сверл используем крутое восхождение,
Рассчитаем произведение biJi (строка 8, таблица 6.14). Наибольшим является произведение  , поэтому фактор
, поэтому фактор  принимаем за базовый
принимаем за базовый 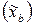 . Выбираем значение параметра λ=λ
. Выбираем значение параметра λ=λ для первого шага при μ = 0,8. По уравнению (6.19) найдем λ (строка 9 , таблица 6.14): λ=0,8/126=0,00635.
для первого шага при μ = 0,8. По уравнению (6.19) найдем λ (строка 9 , таблица 6.14): λ=0,8/126=0,00635.
Вычисляем шаги и координаты первой точки крутого восхождения по уравнениям (6.21):
 = 4
= 4 ;
;  136о
136о
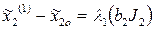 = 4
= 4 ;
;  20о
20о
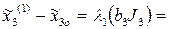 0,07мм;
0,07мм; 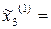 0,92 мм
0,92 мм
Координаты последующих точек на этой линии находим по уравнениям (6.20). Далее выполняем опыты на линии восхождения. Результаты опыта заносим в последний столбец таблицы
Реализация опытов проводилась со второго шага, таккаккоординаты точекx1, x2, x3 на первом шаге почти совпадают со значениями факторов на верхнем уровне.
Результаты опытов 2 и 3 дали наибольшее значение стойкости сверл, что соответствует значениям параметров 2φ=144-148o, α=28o-32o, k=1,1-1,2 мм. Нижний уровень значений параметров в эксперименте дал среднее значение стойкости 257 отверстий, в то время как оптимальные значения параметров дают стойкость в пределах 1600 - 1700 отверстий, т.е. в 6,5 раза больше. Уточнение оптимальных значений параметров возможно путем исследования достигнутой области оптимума c помощью планирования второго порядка [12].
Таблица 6.14
| . | Последова- тельность операций крутого восхождения |  Исследуемые факторы
ду^е ф^торц . , Исследуемые факторы
ду^е ф^торц . ,
| |||
Угол при вершине 
|
Задний угол
α
| Толщина сердцевины k, мм | Стойкость отвер. стия | ||
Основной уровень  Интервал варьирования
Интервал варьирования
 Верхний уровень
Нижний уровень
Верхний уровень
Нижний уровень
| 0,85 0,10 0,95 0,75 | ||||
| Кодовое значение переменных | Х1 | Х2. | Х3 |
Y
| |
| Опыты 1 2 | - + + | - - + | - + - | ||
| 8 . | - + - - + | - - + + + | + - - + + | ||
bi
bi Ji

| 0,8/126 | 9,7 | - - - | ||
 опыты на линии
восхождения
опыты на линии
восхождения
| 0,07 0,99 1,06 1,2 | ||||
Примечание.  Среднее из трех испытаний. Среднее из трех испытаний.
|