Движение по градиенту

Метод крутого восхождения.

 

После вывода уравнения регрессии с помощью постановки полного или дробного факторного эксперимента у экспериментатора может возникнуть следующий вопрос: можно ли оптимизировать полученную функцию отклика, т.е. добиться такого сочетания факторов, при котором полученная функция принимала бы оптимальные значения?

Для поиска оптимальных условий в планировании экстремальных экспериментов широко применяется метод крутого восхождения по поверхности отклика в направлении градиента линейного приближения, который определяется реализацией плана полного или дробного факторного эксперимента.

Пример 8.6. Представим, что человек с закрытыми глазами хочет пройти кратчайшим путем к вершине горы. Он будет делать шаги в разные стороны, чтобы определить направление движения. Достигнув вершины, человек должен оценить ее крутизну, сделав поочередно по шагу во все четыре стороны.

Градиент функции отклика 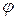есть вектор:

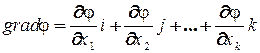(8.15)

или

,

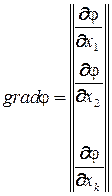где grad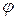- обозначение градиента; 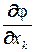- частная производная функции по i-фактору; i, j, … k - единичные векторы в направлении осей факторного пространства.

Следовательно, составляющие градиента являются частными производными функции отклика. В случае, если модель линейна по параметрам, частные производные равны коэффициентам регрессии при факторах. Для движения по градиенту необходимо изменять факторы пропорционально соответствующим коэффициентам регрессии и в ту сторону, в которую указывает знак коэффициентов.

Рассмотрим простейший случай для одного фактора. Пусть регрессионная модель имеет вид:

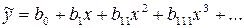
Градиент этой функции в точке x в соответствии с формулой можно записать так:

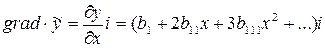
В начале координат (в точке x=0) 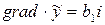, т.е. вектор-градиент функции имеет длину, равную абсолютному значению коэффициента b₁ . На рис.6.6 представлена графическая иллюстрация вектора-градиента для этого случая.

y

В

 

O A

I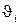

 

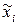
-1 0 +1