И математическая модель.

Полный факторный эксперимент

 

Вернемся к матрице 2². Для движения к точке оптимума нужна линейная модель y = b₀ + b₁x₁ + b₂x₂ . Наша цель - найти по результатам эксперимента значения неизвестных коэффициентов модели. До сих пор, говоря о линейной модели сил, не останавливались на важном вопросе о статистической оценке ее коэффициентов. Теперь необходимо сделать ряд замечаний по этому поводу. 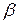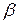Можно утверждать, что эксперимент проводится для проверки гипотезы о том, что линейная модель =₀+₁x₁+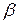₂x₂ адекватна. Греческие буквы использованы для обозначения "истинных" генеральных значений соответствующих неизвестных. Эксперимент, содержащий конечное число опытов, позволяет получить только выборочные оценки для коэффициентов уравнения y = b₀ + b₁x₁ + b₂x₂ .

Не говоря пока о точности и надежности оценок, займемся вычислением оценок коэффициентов. Их можно рассчитать по формуле: b_j = x_ij y_i / N (8.3), j = 0, 1, ... , k .

Обоснование формулы будет дано позднее.

Воспользуемся этой формулой для подсчета коэффициентов b₁ и b₂ для матрицы 2²: b₁ = [(-1)y₁ + (+1)y₂ + (-1)y₃ + (-1)y₄] / 4 ;

b₂ = [(-1)y₁ + (-1)y₂ + (+1)y₃ + (+1)y₄] / 4 ;

Благодаря кодированию факторов расчет коэффициентов превратился в простую арифметическую процедуру. Для подсчета коэффициента b₁ используется вектор-столбец X₁, а для b₂ – X₂. Остается определить b₀. Если уравнение y = b₀ + b₁x₁ + b₂x₂ справедливо, то оно верно и для средних арифметических значений переменных: ₀ = b₀ + b₁₁ + b₂₂. Но в силу свойства симметрии ₁ = ₂ =0 ₀ = b₀ , т.е. b₀ есть среднее арифметическое значение параметра оптимизации. Чтобы его получить, необходимо сложить все y_i и разделить их на число опытов. Чтобы привести эту процедуру в соответствие с формулой для вычисления коэффициентов, в матрицу планирования удобно ввести вектор-столбец фиктивной переменной X₀, которая принимает во всех опытах значение (+1). Это было уже учтено в записи формулы (8.3), где j принимало значение от 0до k..Теперь можно найти все коэффициенты линейной модели y = b₀ + b₁x₁ + b₂x₂ .

Пример 8.1. Исследуется влияние различных факторов на разностенность изделия при вытяжке с утонением в среднем сечении (рис.6).

 

а а

 

 

Рис.6 Эскиз исследуемой детали

 

 

В качестве независимых переменных выбраны следующие факторы; X₁ -угол вытяжной матрицы;Х₂- угол между осью пуансона и направлением хода ползуна; Х₃ - разностенность заготовки в среднем сечении. По условиям проведения эксперимента составлена таблица. (8.4)