Доверительный интервал. Доверительная вероятность.
В предыдущем параграфе мы рассмотрели вопрос об оценке неизвестного параметра  одним числом. Такая оценка называется точечной. В ряде задач требуется не только найти для параметра
одним числом. Такая оценка называется точечной. В ряде задач требуется не только найти для параметра  подходящее численное значение, но и оценить его точность и надежность. Требуется знать - к каким ошибкам может привести замена параметра его точечной оценкой
подходящее численное значение, но и оценить его точность и надежность. Требуется знать - к каким ошибкам может привести замена параметра его точечной оценкой 
 и с какой степенью уверенности можно ожидать, что эти ошибки не выйдут за известные пределы. Такого рода задачи особенно актуальны при малом числе наблюдений, когда точечная оценка
и с какой степенью уверенности можно ожидать, что эти ошибки не выйдут за известные пределы. Такого рода задачи особенно актуальны при малом числе наблюдений, когда точечная оценка 
 в значительной мере случайна и замена
в значительной мере случайна и замена  на
на 
 может привести к серьезным ошибкам. Чтобы дать представление о точности и надежности оценки
может привести к серьезным ошибкам. Чтобы дать представление о точности и надежности оценки 
 , в математической статистике пользуются так называемыми доверительными вероятностями и доверительными интервалами.
, в математической статистике пользуются так называемыми доверительными вероятностями и доверительными интервалами.
Пусть для параметра  получена из опыта несмещенная оценка
получена из опыта несмещенная оценка 
 . Необходимо оценить возможную при этом ошибку. Назначим некоторую достаточно большую вероятность
. Необходимо оценить возможную при этом ошибку. Назначим некоторую достаточно большую вероятность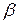 (например,
(например, 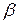 = 0,95 ; 0,99 или 0,99) такую, что событие с вероятностью
= 0,95 ; 0,99 или 0,99) такую, что событие с вероятностью 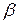 можно считать практически достоверным и найдем такое значение
можно считать практически достоверным и найдем такое значение  , для которого
, для которого
Р(|
 -
-  | <
| <  ) =
) = 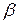
Тогда диапазон практически возможных значений ошибки, возникающей при замене  на
на 
 будет
будет 
 ; большие по абсолютной величине ошибки будут появляться только с малой вероятностью
; большие по абсолютной величине ошибки будут появляться только с малой вероятностью  = 1-
= 1- 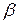 . Перепишем следующее уравнение в следующем виде:
. Перепишем следующее уравнение в следующем виде:
P(
 -
- <
<  <
< 
 +
+  ) =
) = 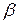


Равенство 
 означает, что с вероятностью
означает, что с вероятностью 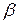 неизвестное значение параметра
неизвестное значение параметра попадает в интервал
попадает в интервал
I =(
=(
 -
- ,
,
 +
+  ).
).













 I
I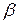





 0
0 
 1
1 



 2
2
Для нахождения доверительных интервалов необходимо знать заранее вид закона распределения величины X. Идея точных методов построения доверительных интервалов сводится к следующему. Любой доверительный интервал находится из условия, выражающего вероятность выполнения некоторых неравенств, в которые входит интересующая нас оценка 
 . Закон распределения оценки
. Закон распределения оценки 
 в общем случае зависит от самих неизвестных параметров величины X. Однако, иногда удается перейти в неравенствах от случайной величины X к какой-либо другой функции наблюденных значений x1,x2,... ,xn закон распределения которой не зависит от неизвестных параметров, а зависит только от числа опытов n и от закона распределения величины X. Такого рода случайные величины играют большую роль в математической статистике; они наиболее подробно изучены для случая нормального распределения величины X.
в общем случае зависит от самих неизвестных параметров величины X. Однако, иногда удается перейти в неравенствах от случайной величины X к какой-либо другой функции наблюденных значений x1,x2,... ,xn закон распределения которой не зависит от неизвестных параметров, а зависит только от числа опытов n и от закона распределения величины X. Такого рода случайные величины играют большую роль в математической статистике; они наиболее подробно изучены для случая нормального распределения величины X.
Например, доказано, что при нормальном распределении величины X случайная величина t =[ -М(x)]/
-М(x)]/ 
подчиняется так называемому закону распределения Стьюдента, где:
 / n ;
/ n ;  = S/
= S/ .
.
Исходя из этого уравнение  , можно записать в следующем виде: P (
, можно записать в следующем виде: P ( -
-  < M ( x ) <
< M ( x ) <  +
+  ) =
) = 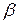 ;
;
Величина t,которая табулирована, определяется с помощью функции Лапласа. Например, если 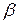 - уровень доверительной вероятности - принят равным 0,95, то величина t
- уровень доверительной вероятности - принят равным 0,95, то величина t = 1,96. Следовательно, доверительный интервал будет иметь начальную точку M (x) –1,96 S /
= 1,96. Следовательно, доверительный интервал будет иметь начальную точку M (x) –1,96 S /  и конечную точку M (x) + 1,96 S /
и конечную точку M (x) + 1,96 S /  .
.
Внутри этого интервала будет находится неизвестное значение M(x) с вероятностью 0,95.
Примечание. Использование функции Лапласа для нахождения доверительных границ возможно лишь при n > 25. Для n < 25 необходимо использовать таблицы распределения Стьюдента.
Рассмотрим определение доверительных интервалов для оценки 2 и
2 и  . Для оценки
. Для оценки  2 используется распределение Пирсона
2 используется распределение Пирсона  2, которое также табулировано. Задавшись вероятностью
2, которое также табулировано. Задавшись вероятностью 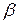 и определив величину q = 1-
и определив величину q = 1- 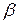 , определяют два значения
, определяют два значения  2. Одно- для вероятности P1 = 1 – q /2, обозначив его
2. Одно- для вероятности P1 = 1 – q /2, обозначив его  , другое - для вероятности P2 = q / 2 -
, другое - для вероятности P2 = q / 2 - .
.
Доверительные границы определяются, исходя из неравенства:
nS2/ <
<  2 < nS2 /
2 < nS2 / 
Доверительные границы для  с той же доверительной вероятностью определяются из неравенства:
с той же доверительной вероятностью определяются из неравенства:
nS / 2 < nS /
2 < nS /  1 .
1 .
Примечание. Указанные способы определения доверительных границ могут быть применены и для случая, когда распределение случайной величины неизвестно заранее. Однако в этом случае границы будут определены лишь грубо, приближенно.