Несмещенные и эффективные оценки характеристики.
Выборочные характеристики. Состоятельные,
В начале курса были рассмотрены такие понятия как классическая и статистическая вероятности.
Если классическая вероятность - это теоретическая характеристика, которую можно определить, не прибегая к опыту, то статистическая вероятность может быть определена только по результатам эксперимента. При большем числе опытов величина W(A) может служить оценкой для вероятности P(A). Достаточно вспомнить классические опыты Бюффона и Пирсона. Подобные аналогии можно продолжить и далее. Например, для теоретической характеристики М(x) таковой аналогией будет  -среднее арифметическое:
-среднее арифметическое:
 =
= 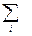
 ifi / n,
ifi / n,
для дисперсии D(x) эмпирическим аналогом будет статистическая дисперсия :
S2(x) = 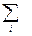 (xi -
(xi -  )2fi / n.
)2fi / n.
Эмпирические характеристики  , S2(x), W(A) являются оценками параметров М(x), D(x), P(A). В тех случаях, когда эмпирические характеристики определяются на основе большого числа опытов, использование их в качестве теоретических параметров не приведет к существенным ошибкам в исследовании, однако в тех случаях, когда число опытов ограничено, ошибка при замене будет существенна. Поэтому к эмпирическим характеристикам, являющимися оценками теоретических параметров предъявляются 3 требования:
, S2(x), W(A) являются оценками параметров М(x), D(x), P(A). В тех случаях, когда эмпирические характеристики определяются на основе большого числа опытов, использование их в качестве теоретических параметров не приведет к существенным ошибкам в исследовании, однако в тех случаях, когда число опытов ограничено, ошибка при замене будет существенна. Поэтому к эмпирическим характеристикам, являющимися оценками теоретических параметров предъявляются 3 требования:
оценки должны быть состоятельными, несмещенными и эффективными.
Оценка называется состоятельной, если вероятность отклонения ее от оцениваемого параметра на величину меньшую как угодно малого положительного числа  стремится к единице при неограниченном увеличении числа наблюдений n,т.е.
стремится к единице при неограниченном увеличении числа наблюдений n,т.е.
P( |
 -
-  | <
| <  ) = 1
) = 1
где  - некоторый параметр генеральной совокупности,
- некоторый параметр генеральной совокупности,
 /- оценка этого параметра. Большинство оценок различных числовых параметров отвечают этим требованиям. Однако одного этого требования бывает недостаточно. Необходимо, чтобы они еще были и несмещенными.
/- оценка этого параметра. Большинство оценок различных числовых параметров отвечают этим требованиям. Однако одного этого требования бывает недостаточно. Необходимо, чтобы они еще были и несмещенными.
Оценка называется несмещенной, если математическое ожидание этой оценки равно оцениваемому параметру:
М ( /) =
/) =  .
.
Примером состоятельной и несмещенной оценки систематического ожидания является средняя арифметическая:
М ( ) =
) =  .
.
Примером состоятельной и смещенной оценки является
дисперсия:
М ( S2(x) ) = [(n – 1)/ n]D(x).
Поэтому, чтобы получить несмещенную оценку теоретической дисперсии D(x) надо эмпирическую дисперсию S2(x) умножить на n/(n – 1) , т.е.
S2(x) = 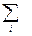 (xi -
(xi -  )2fi / n
)2fi / n n /(n – 1) =
n /(n – 1) = 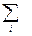 (xi -
(xi -  )2fi/(n – 1).
)2fi/(n – 1).
Практически эту поправку вносят при вычислении оценки дисперсии в тех случаях, когда n < 30 .
Состоятельных несмещенных оценок может быть несколько. Например, для оценки центра рассеивания нормального распределения наряду со средней арифметической  , может быть взята медиана
, может быть взята медиана  . Медиана так же, как и
. Медиана так же, как и  является несмещенной состоятельной оценкой центра группирования. Из двух состоятельных несмещенных оценок для одного и того же параметра естественно отдать предпочтение той, у которой дисперсия меньше.
является несмещенной состоятельной оценкой центра группирования. Из двух состоятельных несмещенных оценок для одного и того же параметра естественно отдать предпочтение той, у которой дисперсия меньше.
Такая оценка, у которой дисперсия будет наименьшей относительно оцениваемого параметра, называется эффективной. Например, из двух оценок центра рассеивания нормального распределения М(x) эффективной оценкой является  , а не
, а не  , так как дисперсия
, так как дисперсия  меньше дисперсии
меньше дисперсии  . Сравнительная эффективность этих оценок при большой выборке приближенно равна: D(
. Сравнительная эффективность этих оценок при большой выборке приближенно равна: D( ) / D
) / D = 2/
= 2/ = 0,6366.
= 0,6366.
Практически это означает, что центр распределения генеральной совокупности (назовем его 0 ) определяется по
0 ) определяется по с той же точностью при n наблюдениях, как и при 0,6366 n наблюдениях по средней арифметической
с той же точностью при n наблюдениях, как и при 0,6366 n наблюдениях по средней арифметической  .
.
4.4. Свойства выборочных средних и дисперсий.
1. Если объем выборки достаточно велик, то на основе закона больших чисел с вероятностью близкой к единице, можно утверждать, что средняя арифметическая  и дисперсия S2 будут как угодно мало отличаться от М(x) и D(x), т.е.
и дисперсия S2 будут как угодно мало отличаться от М(x) и D(x), т.е.

 М(x), S2(x)
М(x), S2(x)  D(x),
D(x),
2. Ошибка вычисления М(x) по средней  выборки зависит от ее объема n и равна
выборки зависит от ее объема n и равна  S /
S /  .
.
Ошибка вычисления среднеквадратического отклонения генеральной совокупности по среднеквадратическому отклонению выборки зависит от ее объема и равна  S /
S /  .
.
3. Если случайная величина X в генеральной совокупности имеет нормальное распределение со средней М(x) и дисперсией D( ) , то и средние арифметические
) , то и средние арифметические  выборок из этой совокупности будут подчинены также нормальному распределению со средней
выборок из этой совокупности будут подчинены также нормальному распределению со средней  и дисперсией D(
и дисперсией D( ), каков бы не был объем выборок n, лишь бы число выборок было достаточно велико.
), каков бы не был объем выборок n, лишь бы число выборок было достаточно велико.
4. Когда дисперсия D(x), генеральной совокупности неизвестна, тогда для больших значений n с большей вероятностью малой ошибки можно дисперсию выборочных средних вычислить приближенно по равенству:
D( ) = S2(x) / n,
) = S2(x) / n,
где S2(x) = 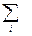 (xi -
(xi -  )2fi / n- дисперсия большой выборки.
)2fi / n- дисперсия большой выборки.