ОСНОВЫ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ

Рис. 2.10 Уклон и конусность

Уклон

Рисунок 2.9 Смешанное сопряжение двух дуг

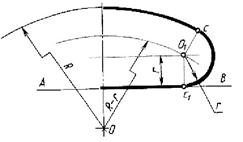
Рисунок 2.6 Сопряжения угла с дугой окружности

Сопряжение прямой с дугой окружности с внешним касанием (рис. 2.7 а) Параллельно заданной прямой АВ на расстоянии, равном радиусу r (радиус сопрягающей дуги), проводим прямую ab. Из центра Опроводим дугу окружности радиусом R + r до пересече­ния ее с прямой ab в точкеО₁(цент­р дуги сопряжения). Точку сопряжения с находим на пересечении прямой ОО₁с дугой окружности радиуса R. Точка сопряжения с₁, является основанием перпендикуляра, опущенного из центра О₁ на данную прямую АВ.

б)

а)

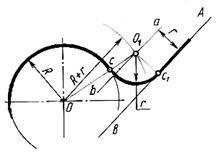
Рисунок 2.7 Сопряжения прямой с дугой окружности с внешним касанием (а) и с внутренним касанием (б)

Сопряжение прямой с дугой окружности с внутренним касанием(рис. 2.7 б) Центр дуги сопряжения О₁находим на пересечении вспомогательной прямой, проведенной параллельно данной прямой на расстоянии r, с дугой вспомогатель­ной окружности, описанной из центра О радиусом, рав­ным R -r . Точка сопряжения с₁ является основанием перпендикуляра, опущенного из точки О₁ на данную прямую. Точку сопряжения с находим на пересечении прямой ОО₁с сопрягаемой дугой.

Внутреннее сопряжение двух дуг (рис. 2.8 а) Центры О и О₁ сопрягаемых дуг находятся внутри сопрягающей дуги радиуса R. Из центра Опро­водим вспомогательную дугу радиусом R – R₁, а из центра О₁ - радиусом R - R₂. Вспомогательные дуги пересекутся в точке О₂, (центр сопрягающей дуги). Для нахождения точек сопряжения точку О₂ соеди­няем с точками О и О₁ прямыми линиями. Точки s и s₁ - точки пере­сечения продолжения прямых О₂О и О₂О₁ с сопрягае­мыми дугами - являются точками сопряжения.

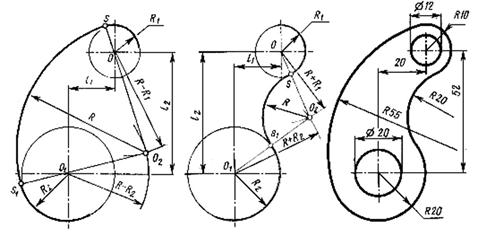
а) б) в)

Рисунок 2.8 Сопряжение двух дуг: внутреннее (а), внешнее (б), пример детали с внутренним и внешним сопряжением (в)

Внешнее сопряжение двух дуг (рис. 2.8 б)Центры О и О₁ сопрягаемых дуг радиусов R₁ и R₂ находятся вне сопрягающей дуги радиуса R. Из центра О проводим вспомогательную дугу радиусом R +R₁, а из центра О₁ — радиусом R + R_2. Вспо­могательные дуги пересекутся в точке О₂, - центр сопрягающей дуги. Для нахождения точек сопряжения центры дуг соединяем прямыми линиями ОО₂ и О₁О_2. Эти две пря­мые пересекают сопрягаемые дуги в точках сопряже­ния s и s₁ .

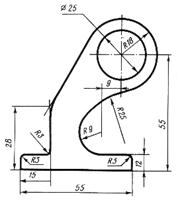Смешанное сопряжение двух дуг(рис. 2.9)Центр О₁ одной из сопрягаемых дуг лежит внутри сопрягающей дуги радиуса R, а центр Одругой сопрягаемой дуги вне ее. Из центра О проводим вспомогательную дугу радиусом, равным R +R₁, а из центра О₁ — радиусом, R- R₂ Вспомогательные дуги пересекутся в точке О₂- центр сопряга­ющей дуги. Соединив точки О и О₂ прямой, получаем точку сопряжения s₁,соединив точки О₁ и О₂находим точку сопряжения s. Из центра О₂ проводим дугу сопряжения от sдо s₁ .

Уклон –характеризует наклон прямой линии. Обозначается на чертежах знаком (рис. 2.10, а, б)) . Угол знака направлен в ту же сторону, сто и угол уклона. Задается отношением катетов прямоугольного треугольника (рис.2.10,а) или в процентах (рис. 2.10, б). Например, уклон 1:3, где длина вертикального катета принята за 1, а по горизонтали отложено три отрезка, равных вертикальному катету. При обозначении процентами вертикальный катет имеет длину в указанных процентах от горизонтального катета.

а) б) в) г)

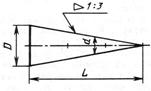
Конусность (С)–это отношение разности диаметров двух поперечных сечений конуса к расстоянию между ними. (рис. 2.10, в).Для конуса 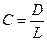(рис. 2.11, г). Конусность обозначается знакоми задается так же, как и уклон отношением D/L, где значение D принято за 1.