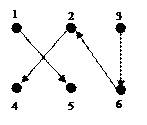Основные законы алгебры множеств
Алгебра множеств
Условные приоритеты операций над множествами
С целью упрощения записи формул принято руководствоваться следующим правилом экономии скобок:
при отсутствии скобок порядок выполнения операций над множествами определяется последовательностью:
Ø,\, Å, I , U .
(теоретико-множественный аналог алгебры действительных чисел)
Алгебра множеств –совокупность тождеств, справедливых независимо от того, какое универсальное множество и какие именно его подмножества входят в эти равенства.
1) Коммутативные (переместительные) законы
А È В = В È А
А Ç В = В Ç А
А D В = В D А
2) Ассоциативные (сочетательные) законы
А È (В È С) = (А È В) È С
А Ç (В Ç С) = (А Ç В) Ç С
3)Дистрибутивные (распределительные) законы
А È (В Ç С) = (А È В) Ç (А È С)
А Ç (В È С) = (А Ç В) È (А Ç С)
4)Законы с Æ и U
А È Æ = А А Ç U = А А È = U
= U
А Ç Æ = Æ А È U = U А Ç = Æ
= Æ
 = Æ
= Æ  = U
= U
6) Законы идемпотентности
А Ç А = А А È А = А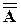 = А
= А
7) Законы поглощения
А È (А Ç В) = А
А Ç (А È В) = А
8) Законы де Моргана
 =
=  È
È 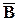
 =
=  Ç
Ç 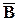
9) Законы склеивания
(А Ç В) È ( Ç В) = В
Ç В) = В
(А È В) Ç ( È В) = В
È В) = В
Лекция №2: Теория отношений
Кортеж, набор, вектор –упорядоченная последовательность элементов, в которой каждый элемент занимает определенное место.
Элементы, образующие вектор, называются координатами или компонентами вектора.
Число координат вектора называется длиной или размерностью вектора.
 – пустой кортеж,
– пустой кортеж,
 – одноэлементный кортеж,
– одноэлементный кортеж,
 – пара, двуэлементный кортеж,
– пара, двуэлементный кортеж,
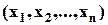 – кортеж длины nили n-ка (“энка”).
– кортеж длины nили n-ка (“энка”).
Прямое (декартово) произведение множеств 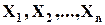 – множество всевозможных упорядоченных наборов
– множество всевозможных упорядоченных наборов  , таких, что первый элемент принадлежит множеству
, таких, что первый элемент принадлежит множеству  , второй – множеству
, второй – множеству  ,
,  -й – множеству
-й – множеству  :
:
 .
.
Декартово произведение  , в котором одно и тоже множество
, в котором одно и тоже множество  умножается
умножается  раз само на себя – декартова степеньмножества
раз само на себя – декартова степеньмножества  :
:  .
.
Прямое (декартово) произведение множеств Х и Y – множество всевозможных упорядоченных пар(двуэлементных кортежей), таких что:
Х x Y = {(x,y) | xÎX, yÎY}.
При  множество
множество 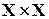 называется декартовой степеньюмножества Xи обозначается X2.
называется декартовой степеньюмножества Xи обозначается X2.
Например:
Пусть 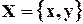 ,
, 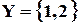 , тогда
, тогда  ,
,  .
.
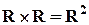 – множество точек плоскости,
– множество точек плоскости, 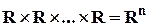 – множество точек
– множество точек  -мерного пространства.
-мерного пространства.
Шахматная доска: 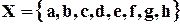 ,
,  ,
, 
Некоторые свойства прямого произведения:
1) 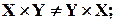
2)  ;
;
3) 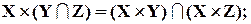
4) 
 - арное отношение
- арное отношение 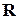 на множествах
на множествах  – это всякое, произвольное подмножество декартова произведения этих множеств:
– это всякое, произвольное подмножество декартова произведения этих множеств:
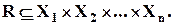
Если набор элементов 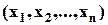 принадлежит отношению
принадлежит отношению 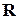 , то говорят, что элементы
, то говорят, что элементы 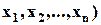 находятся в отношении
находятся в отношении 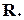
 - арное отношение
- арное отношение 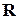 на множестве
на множестве  – это всякое, произвольное подмножество
– это всякое, произвольное подмножество  - й декартовой степени этого множества:
- й декартовой степени этого множества: 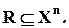
Бинарное отношение на множествах X и Y – произвольное подмножество прямого произведения двух множеств:
r Í Х x Y = {(x,y) | xÎX, yÎY}.
Если r Í Х2, то говорят, что отношение r задано на множестве Х.
Если (x,y)Îr,то говорят, что (x,y) находятся в отношении rили связаны отношением r: х r yили y = r(х).
Область определения Drбинарного отношения – множество первых координат каждой упорядоченной пары отношения  :
:
Dr = { x | (x,y) Î r }.
Область значений Jrбинарного отношения – множество вторых координат каждой упорядоченной пары отношения  :
:
J r = { y | (x, y) Î r }.
Способы задания отношений
1) Список пар или характеристическое свойство.
Любое бинарное отношение (как множество) может быть задано в виде списка пар, из которых состоит отношение, или с использованием характеристического или определяющего свойства.
r = { (1,1), (2,2), (3,3), (4,4)}на r Í Х2, Х= {1,2,3,4} или
 }.
}.
2) Матрица отношения.
В матрице отношения строки отвечают элементам множества  , столбцы элементам множества
, столбцы элементам множества  , элемент матрицы равен:
, элемент матрицы равен:
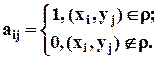
Если 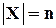 , а
, а 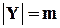 , то матрица отношения имеет размерность
, то матрица отношения имеет размерность 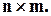
r ={(1,1), (2,2), (3,3), (4,4)} на r Í Х2, Х= {1,2,3,4}.
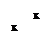
| ||||||
| ||||||
3) Графическое изображение отношений.
На плоскости изображаются точками элементы множеств 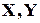 . Если пара
. Если пара  принадлежит отношению, то соединяются точки, изображающие
принадлежит отношению, то соединяются точки, изображающие  , линией, направленной от первого элемента ко второму. Обозначая таким образом все пары, принадлежащие отношению, получаем фигуру, которая называется графом отношения.
, линией, направленной от первого элемента ко второму. Обозначая таким образом все пары, принадлежащие отношению, получаем фигуру, которая называется графом отношения.
r ={(1,5), (2,4), (3,6), (6,2)} на r Í Х2, Х= {1,2,3,4,5,6}.