Операции над множествами

Объединение множеств A и B (обозначается A È B) – множество, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств, т.е.

A B

A È B = {а ½ а ÎA или а Î B}.

 

 

Пересечениемножеств A и B (обозначается А∩ B) – множество, состоящее из всех элементов, принадлежащих каждому из этих множеств, т.е.

A B

А ∩ B = {а ½а ÎАи а Î B}.

 

 

A B

Разность множеств А и B (обозначается А \ B) – множество, состоящее из всех элементов множества A, не принадлежащих множеству B, т.е.

А \ B={а ½а ÎА и а Ï B}.

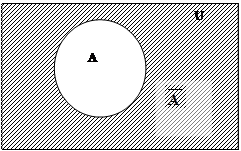Дополнениемножества А в универсальном множестве U(обозначается , ØА)– множество, состоящее из всех элементов универсального множества U, не принадлежащих множеству А, т.е. ØА = U \ A.

Симметрическая разность множеств A и B(обозначается A Å B или A D B) – множество, состоящее из всех элементов, принадлежащих в точности одному из этих множеств, т.е.

ADB = {а½ либо а Î A и а Ï B, либо а Ï A и а Î B}

A D B = (A \ B)È (B \ A) = (AÈB) \ (AÇB)