Интегральная функция распределения вероятностей случайной величины
ТЗР-3. Интегральная функция распределения вероятностей СВ
Это наиболее универсальный способ задания закона распределения. Его можно применять и для дискретных и для непрерывных СВ. Часто, говоря об этом способе, слова «интегральная» и «вероятностей» отбрасывают и используют термин «функция распределения СВ» .
Интегральная функция распределения вероятностей представляет собой вероятность того, что некоторая случайная величина Х принимает значение меньшее, чем текущее х:
F(х) = Р(Х < х) (20)
Например, если для такой СВ, как ток в ЛЭП, функция распределения F(90) = 0,3, то это означает, что вероятность принятия током в ЛЭП значения, меньше 90 А, равна 0,3.
Если для напряжения в сети функция распределения F(215) = 0,4, то 0,4 –это вероятность того, что напряжение в сети меньше 215 В.
Функция распределения вероятностей может быть задана аналитически, таблично или графически.
Пример 27
По заданному ряду распределения оценок студентов на экзамене (табл. 8, строки 1 и 2) записать интегральную функцию распределения (табл. 8, строка 3) и построить её график.
Таблица 8. Ряд и интегральная функция распределения оценок на экзамене
| Оценка Х | |||||
| Вероятность | 0,1 | 0,5 | 0,3 | 0,1 | - |
| Функция распределения F(х) | 0,1 | 0,6 | 0,9 | 1,0 |
Для нахождения значений функции распределения необходимо воспользоваться её определением (20):
· для Х = 2 F(2)= Р(Х <2) = 0, так как оценок меньше 2 на экзамене не бывает;
· для Х= 3 F(3)= Р(Х <3) = Р(Х = 2) = 0,1, т.к. меньше 3 есть только оценка 2;
· для Х = 4 F(4)= Р(Х <4) = Р(Х= 2) + Р(Х= 3) = 0,1 + 0,5 = 0,6, т.к. меньше 4 есть две оценки – 2 или 3 (получение оценки меньше 4 равнозначно получению или оценки 2 или оценки 3 и для нахождения F(4) можно воспользоваться формулой сложения вероятностей несовместных событий);
· для Х = 5 F(5)= Р(Х <5) = Р(Х <4) + Р(Х= 4) = 0,6 + 0,3 = 0,9, то есть к F(4) добавляется вероятность того, что оценка равна 4.
Анализируя порядок нахождения значений F(х), видим, что к вероятности наименьшего значения СВ сначала добавляется вероятность второго значения, затем – третьего и т.д. То есть вероятности как бы накапливаются. Поэтому интегральную функцию распределения иначе называют «функцией накопленных вероятностей».
В литературе по статистике функцию накопленных вероятностей достаточно часто называют кумулятой.
На основе данных табл. 8 может быть построен график интегральной функции дискретной случайной величины (рис. 29). Эта функция является разрывной. Скачки соответствуют отдельным дискретным значениям Х, а высоты «ступенек» - соответствующим вероятностям. В местах разрыва функция (рис. 29) принимает значения обозначенные точками, т.е. непрерывна слева. В общем виде для дискретной СВ можно записать: F(х) = Р(Х < х) =
. (21)
Для того чтобы понять, как будет выглядеть график интегральной функции распределения для непрерывной СВ, можно прибегнуть к следующим рассуждениям. Если представить, что количество значений дискретной СВ возрастает, то мест разрыва будет становиться больше, а высота ступенек будет уменьшаться. В пределе, когда количество возможных значений станет бесконечным (а это и есть непрерывная СВ), ступенчатый график превратится в непрерывный (рис. 30).
Поскольку интегральная функция распределения вероятностей СВ имеет первостепенное значение, рассмотрим подробнее ее свойства:
Свойство 1. Такой способ задания закона распределения универсален, т. к. пригоден для задания закона распределения как дискретных, так и непрерывных СВ.
Свойство 2. Поскольку интегральная функция распределения – это вероятность, то ее значения лежат на отрезке от 0 до 1.
Свойство 3. Функция распределения безразмерна, как и любая вероятность.
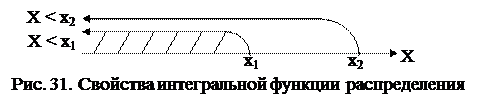Свойство 4. Функция распределения есть неубывающая функция, т. е. большему значению аргумента соответствует то же или большее значение функции: при х2 > х1 F(х2) ≥ F(х1).
Это свойство вытекает из того (рис. 31), что вероятность попадания на больший отрезок (от -∞ до х2) никак не может быть меньше вероятности попадания на меньший отрезок (от -∞ до х1).
Если на участке от х2до х1(рис. 32)нет возможных значений СВ (это возможно для дискретных СВ), то F(х2) = F(х1).
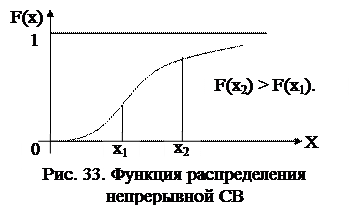
Для функции распределения непрерывной СВ (рис.33) F(х2) всегда больше F(х1).
Свойство 4 имеет два следствия.
Следствие 1
Вероятность того, что величина Х примет значение в интервале (х1;х2) равна разности значений интегральной функции на границах интервала:
Р(х1 ≤ Х < х2) = F(х2) – F(х1). (15)
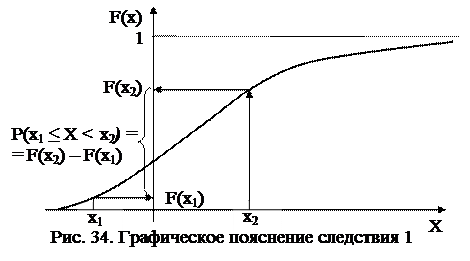Это следствие можно пояснить следующим образом (рис.31):
F(х2) = Р(Х < х2) –
вероятность того, что СВ принимает значения левее точки х2.
F(х1) = Р(Х < х1) – вероятность того, что СВ принимает значения левее точки х1.
Отсюда разность
Р(Х < х2) - Р(Х < х1) есть вероятность того, что значения СВ расположены на участке от х1 до х2 (рис.34).