Лекция 1.

ЖЕСТКОСТНЫЕ ХАРАКТЕРИСТИКИ УПРУГИХ ЭЛЕМЕНТОВ КОНСТРУКЦИИ

Прочность– способность конструкции выдерживать заданную нагрузку, не разрушаясь.

Жесткость– способность конструкции препятствовать изменению формы под действием нагрузки.

 

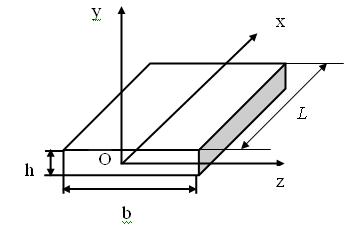
Рассмотрим жесткостные характеристики прямолинейного стержня.

 

Приложим в полюсе систему сил

, а также

моментов _..

Обозначим:

 

–поступательное

 

перемещение полюса (т.О);

 

– угловое перемещение полюса (т.О).

 

Заметим, что положительным направлением для моментов и углов поворота является направление против часовой стрелки.

 

; ;

;

; ;

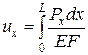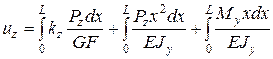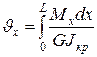, (1.1)

 

 

где - модуль упругости I-го рода (модуль Юнга);

 

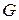- модуль упругости II-го рода (модуль упругости при сдвиге);

 

- площадь плоского сечения;

 

, - моменты инерции плоских сечений относительно осей Oy, Oz;

 

- момент инерции при кручении;

 

, - коэффициенты формы при сдвиге;

 

;

;

;

 

 

( для прямоугольного сечения);

(при ; при )

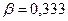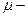; коэффициент Пуассона.

 

 

Введем следующие обозначения:

Обобщенное перемещение:

 

 

 

.

 

Обобщенная сила:

 

 

 

.

 

Запишем перемещение полюса для общего случая формы стержня:

 

;

;

;

;

;

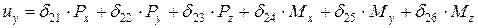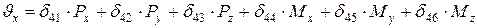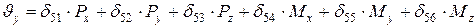. (1.2)

 

Перепишем уравнения перемещения полюса в координатной форме в следующем виде:

(1.3)

 

Мы можем записать их в матричной форме:

; (1.4)

где ; ,

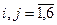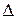- матрица податливости (квадратная матрица размерности (6х6);

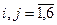() - элементы матрицы податливости.

 

Матрица податливости Δ однозначно и полностью описывает жесткостные характеристики рассматриваемого упругого элемента (в данном случае стержня).

 

Элемент матрицы податливости (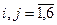) – это величина, численно равная перемещению в -ом направлении при действии единичной силы в -ом направлении:

. (1.5)

 

- диагональные элементы характеризуют податливость стержня в направлении действующей силы ;

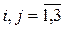при - эти элементы характеризуют линейную податливость стержня (размерность элементов [м/Н] );

при - эти элементы характеризуют угловую податливость стержня (размерность элементов [1/мН] );

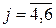при , и при , 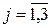- эти элементы характеризуют перекрестные связи между угловыми и линейными перемещениями полюса (размерность элементов [1/Н] ).

 

Интеграл Мора, описывающий перемещение (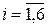) произвольной точки упругого стержня при действии внешней нагрузки,

где 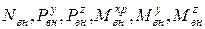- соответствующие внутренние усилия, возникающие от действия внешней нагрузки;

 

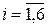() - соответствующие внутренние усилия, возникающие от действия в полюсе единичной нагрузки ().

 

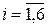На основании интеграла Мора и выражения (1.5) запишем формулу для определения элементов () матрицы податливости:

. (1.6)

 

Согласно выражения (1.6) является очевидным, что ().