VII. Конденсатор в цепи постоянного тока

VI. Зависимость емкости конденсаторов от времени и от температуры

V. Поляризация диэлектриков

IV. Номинальная емкость и допускаемые отклонения

III. Емкость

Система условных обозначений и маркировка конденсаторов

II. Классификация конденсаторов

В зависимости от назначения различают конденсаторы общего и специального назначения. Группа общего назначения включает в себя широко применяемые конденсаторы, используемые в большинстве видов и классов аппаратуры (низковольтные конденсаторы). Все остальные конденсаторы являются специальными. К ним относятся высоковольтные, импульсные, помехоподавляющие, пусковые, дозиметрические и др.

По характеру изменения емкости различают конденсаторы постоянной емкости, переменной емкости и подстроечные. У конденсаторов постояннойемкости – емкость является фиксированной, и в процессе эксплуатации не изменяется. Конденсаторы переменной емкости – допускают изменение емкости в процессе функционирования аппаратуры. Управление емкостью может осуществляться механически, электрическим напряжением (вариконды) и температурой (термоконденсаторы). Емкость подстроечных конденсаторов изменяется при разовой или периодической регулировке и не изменяется в процессе функционирования аппаратуры.

По характеру защиты от внешних факторов конденсаторы выполняются незащищенные, защищенные, неизолированные, изолированные, уплотненные и герметизированные. Незащищенные конденсаторы допускают эксплуатацию в условиях повышенной влажности только в составе герметизированной аппаратуры. Защищенные конденсаторы допускают эксплуатацию в аппаратуре любого исполнения. Неизолированные конденсаторы – не допускают касания своим корпусом шасси аппаратуры. Изолированные конденсаторы имеют хорошее изоляционное покрытие (компаунды, пластмассы и т.д.) и допускают касания корпусом шасси или токоведущих частей аппаратуры. Уплотненные конденсаторы – имеют уплотненную органическими материалами конструкцию корпуса. Герметизированные конденсаторы – имеют герметичную конструкцию корпуса, который исключает возможность сообщения окружающей среды с его внутренним пространством. Герметизация осуществляется с помощью керамических и металлических корпусов или стеклянных колб.

 

Система условных обозначений и маркировка конденсаторов может быть сокращенной и полной.

В соответствии с действующей системой сокращенное условное обозначение состоит из букв и цифр.

Первый элемент – буква или сочетание букв, обозначающее подкласс конденсаторов: К – постоянной емкости; КТ – подстроечные; КП – переменной емкости; КС – конденсаторные сборки.

Второй элемент – цифра, обозначает группу конденсатора в зависимости от материала диэлектрика.

Третий элемент – цифра, пишется через дефис и обозначает регистрационный номер конкретного типа конденсатора. В состав третьего элемента может входить так же буквенное обозначение.

Полное условное обозначение конденсатора состоит из сокращенного обозначения, обозначения и величины основных параметров и характеристик, необходимых для заказа и записи конструкторской документации, обозначения климатического исполнения и документа на поставку.

Например:

- Керамический конденсатор постоянной емкости на номинальное напряжение до 1600 В с регистрационным номером 17 имеет сокращенное условное обозначение К10-17;

- Подстроечный керамический конденсатор с регистрационным номером 25 сокращенно обозначается КТ4-25;

- Конденсатор керамический К10-7В, всеклиматического исполнения с температурным коэффициентом емкости равным , номинальной емкостью 27пФ, с допуском ±10%, поставляемый по ГОСТ 5.621-70 имеет полное условное обозначение:

К10-7В-М47-27пФ±10% ГОСТ 5.621-70

Кодированные обозначения предназначены для маркировки малогабаритных конденсаторов и для записи на малоформатных многоэлементных электрических схемах. Полное обозначение состоит из значения номинальной емкости (цифра) и обозначения единицы измерения (пФ, мкФ, Ф). Например: 1.5 пФ (1П5 или 1p5), 0.1 мкФ, 10 Ф.

 

 

Основное свойство конденсатора – его емкость, то есть способность накапливать на обкладках электрический заряд. Выражается соотношением:

[Ф] [1]

где Q – электрический заряд на обкладках конденсатора в кулонах [Кл];

U – напряжение приложенное к обкладкам [В].

 

Фарада – крупная единица, поэтому для оценки емкости используют меньшие единицы, между которыми существует следующее соотношение:

[2]

 

Емкость конденсатора зависит от его геометрических размеров (от площади обкладок и расстояния между ними) и типа диэлектрика (от величины диэлектрической проницаемости )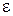

 

Емкость плоского конденсатора выражается формулой:

[Ф], [3]

где S – площадь обкладки [];

h – толщина диэлектрика[м].

 

Для плоского многопластинчатого конденсатора, собранного из N обкладок, соединенных через одну параллельно:

[Ф] , [4]

где h – расстояние между обкладками.

 

Для цилиндрического конденсатора, представляющего собой два коаксиальных проводящих цилиндра, разделенных диэлектриком:

[Ф] , [5]

 

где l-длина обкладок [м];

-диаметр внутреннего электрода [м];

-диаметр наружного электрода [м].

 

 

Для спиральных конденсаторов емкость равна удвоенному значению емкости такого же конденсатора, но развернутого в плоскую длинную ленту:

[Ф] , [6]

где b – ширина обкладок [м];

l – длинна обкладок [м];

h – толщина диэлектрика между обкладками [м].

 

Для шарового конденсатора:

[Ф] , [7]

где r – радиус сферического конденсатора [м].

Эти формулы справедливы для однородного поля, и не учитывают его искажения у края конденсаторных обкладок. Если учитывать искажения, то вводят поправку на краевую емкость .

Конденсаторы соединяют в группы – параллельно, последовательно и смешанно.

При параллельном соединении конденсаторов общая емкость равна сумме емкостей:

[8]

 

При последовательном соединении величина обратная общей емкости группы равна сумме обратных величин отдельных емкостей.

Рис.5

 

[9]

Общая емкость двух последовательно соединенных конденсаторов равна:

[10]

При смешанном соединении конденсаторов общую емкость находят, применяя эти формулы к отдельным участкам цепи.

Конденсатор большей емкости часто собирают из параллельно соединенных одинаковых секций. Если число секций m и емкость каждой секции , то емкость конденсатора равна:

[11]

При последовательном соединении секций:

[12]

 

Если конденсатор собран из «n» последовательно соединенных групп секций, а каждая группа составлена из «m» параллельно соединенных секций, то емкость конденсатора равна:

[13]

 

Номинальная емкость – это емкость, значение которой обозначено на конденсаторе или указано в нормативно – технической документации и является исходным для отсчета допускаемого отклонения.

Номинальные значения емкостей стандартизованы, и выбираются из определенных рядов чисел. Согласно стандарту СЭВ 1076 – 78 установлены семь рядов емкостей: Е3, Е6, Е12, Е24, Е48, Е96, Е192. Цифры после буквы Е указывают число номинальных значений в каждом десятичном интервале (декаде). Например: ряд Е6 содержит шесть значений номинальных емкостей, в каждой декаде, которые соответствуют числам: 1.0; 1.5; 2.2; 3.3; 4.7; 6.8; или числам, полученным путем их умножения или деления на . Чаще используют ряды Е3, Е6, Е12, Е24.

Фактические значения емкостей могут отличаться от номинальных в пределах допускаемых отклонений. По величине допускаемого отклонения емкости от ее номинального значения конденсаторы различаются на следующие основные классы точности /3/

Класс						I	II	III	IV	V	VI
Допуск, %	±0.1	±0.2	±0.5	±1	±2	±5	±10	±20	-10 +20	-20 +30	-20 +50

Для образцовых конденсаторов применяется допуск ± 0.25%.

Допуск по емкости представляет собой относительную разность между измеренной емкостью и номинальной емкостью .

[14]

 

 

Емкость плоского воздушного конденсатора можно вычислить, используя выражение:

[15]

Фарадей обнаружил, что емкость конденсатора увеличивается, если пространство между обкладками конденсатора вместо воздуха частично или полностью заполнить твердым или жидким диэлектриком. Кратность увеличения емкости равна относительной диэлектрической проницаемости этого вещества:

[16]

– абсолютная диэлектрическая проницаемость или удельная емкость материала [Ф/м].

Причиной увеличения емкости является поляризация диэлектрика, то есть перемещение связанных зарядов диэлектрика на ограниченные расстояния под воздействием электрического поля.

Электрическое поле, образованное этими зарядами, направлено навстречу внешнему и ослабляет его. Таким образом, при той же величине заряда на обкладках напряжение между ними при наличии поляризующегося диэлектрика оказывается меньше, а емкость больше.

Различают следующие виды поляризации:

- Электронная – упругое смещение и деформация электронных оболочек

- атомов и ионов. Наблюдается у всех видов диэлектрика, и не связана с потерей энергии.

- Ионная – смещение упруго-связанных ионов.

- Дипольная – частичная ориентация диполей под действием поля. Она связана с тепловым движением частиц, с потерей энергии.

- Структурная или миграционная поляризация – наблюдается в твердых телах неоднородной структуры, а так же при наличии примесей (пропитанные, бумажные, пленочные конденсаторы).

- Спонтанная – характерна для сегнетоэлектриков, характеризуется рассеянием энергии, выделением тепла.

Для конденсаторостроения неполярные вещества не очень удобны вследствие малого значения диэлектрической проницаемости 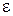, но все же применяются, когда требуются малые потери (), высокое удельное сопротивление и стабильность диэлектрической проницаемости к ним относятся: нефтяное масло, парафин, церезин, полиэтилен, полистирол, фторопласт – 4 и др.

Технические конденсаторные диэлектрики имеют сложную неоднородную структуру, поэтому у них присутствует несколько видов поляризации.

 

 

Значение емкости конденсаторов при различных температурах определяется температурной зависимостью диэлектрической проницаемости диэлектрика, а так же изменением линейных размеров металлических обкладок и диэлектрика. Для оценки температурной зависимости емкости конденсатора служит температурный коэффициент емкости ТКЕ, показывающий, на сколько изменяется емкость при увеличении температуры на 1 .

, [17]

Температурный коэффициент емкости может быть положительным, отрицательным или равным нулю.

Если зависимость емкость от температуры носит линейный характер, то величину температурного коэффициента емкости можно вычислить по формуле:

, [18]

где – емкость при температуре 20. Чаще ТКЕ выражают в миллионных долях изменения емкости (). Если зависимость емкости от температуры нелинейна, то часто указывают относительное изменение емкости при переходе от к :

[%], [19]

Для обозначения группы температурной стабильности конденсатора используют условные обозначения в виде букв, обозначающих знак ТКЕ (М – отрицательный; П – положительный; МП – примерно равен нулю) и цифр, указывающих значение ТКЕ , а так же цветные кодировки.

Характер зависимости емкости конденсатора от температуры обычно определяется характером температурной зависимости диэлектрической проницаемости диэлектрика, то есть . Кроме того, она обусловлена особенностями конструкции конденсатора и изменением его размеров при нагревании.

Для плоского конденсатора с квадратными обкладками, сторона которых равна l, имеем:

[Ф], [20]

где h – толщина диэлектрика;

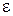– диэлектрическая проницаемость.

Дифференцируя выражение [20] по температуре, получаем:

[21]

Разделив левую и правую части выражения [21] на левую и правую части выражения [20] получим:

[22]

или

[23]

где – температурный коэффициент диэлектрической проницаемости;

– коэффициент линейного расширения металла обкладок;

– коэффициент линейного расширения диэлектрика.

Если в качестве обкладок использован тонкий слой металла, нанесенный непосредственно на поверхность твердого диэлектрика (металлизированный конденсатор), то расширение обкладок конденсатора будет определяться не расширением металла, а расширением диэлектрика. В этом случае и формула [23] примет вид:

[24]

В выражении [23] для обычных металлов и сплавов величина для неорганических и для органических диэлектриков. Поэтому значениями и в формуле [23] можно пренебречь, если имеет значения близкие к пределу и выше.

Современная электроника требует применения конденсаторов с малой зависимостью от температуры, то есть с малым ТКЕ. Для изготовления таких конденсаторов следует применять материалы с возможно меньшим значением , и _. При конструировании часто применяют параллельное и последовательное соединения конденсаторов. Значение ТКЕ системы конденсаторов будет зависеть от соотношения между ТКЕ и емкостями отдельных конденсаторов.

Малые изменения емкости от температуры можно обеспечить, соединив параллельно две секции с разными диэлектриками, имеющими ТКЕ разного знака. Необходимые величины емкостей определяются выражением:

[25]

[26]

[27]

[28]

где С – заданная емкость конденсатора;

и – емкости обоих секций;

и – значения ТКЕ этих секций.

[29]

[30]

Имея конденсаторы с различным знаком ТКЕ, и используя параллельное соединение, последовательное и смешанное можно получать требуемые ТКЕ батарей и, в том числе близкое к нулю.

Условием температурной компенсации является получение ТКЕ близкого к нулю, то есть

[31]

[32]

[33]

При последовательном соединении:

[34]

[35]

[36]

[37]

и условие температурной компенсации выглядит следующим образом:

[38]

Задачу температурной компенсации можно разрешить и с применением одного конденсатора, но с диэлектриком, представляющим собой смесь двух материалов, имеющих различные знаки ТКЕ. Соотношения между толщиной диэлектрика h, диэлектрической проницаемостью 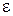и температурным коэффициентом при одной площади обкладок и результирующем ТКЕ = 0 определяются:

- Для параллельного соединения: [39]

- Для последовательного соединения: [40]

Воздействие повышенной или пониженной температур может привести и к необратимым изменениям емкости. Необратимую нестабильность емкости характеризуют величиной (в % от исходного значения) после возвращения к исходной температуре для конденсатора, подвергшегося нагреву или охлаждению или воздействию нескольких температурных циклов.

Необратимые изменения емкости обычно связаны с небольшими остаточными изменениями размеров конденсатора. У конденсаторов с органическим диэлектриком они больше, чем в случае неорганических диэлектриков, так как для органических веществ ТКЕ примерно на один порядок выше, чем у неорганических, что легче приводит к необратимым воздействиям.

Необратимые изменения размеров конденсаторов являются так же одной из основных причин изменения его емкости во времени при длительном хранении. Поэтому величина после нагрева может давать некоторое представление о стабильности емкости во времени.

Значительные изменения 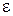во времени наблюдаются только у некоторых видов сегнето-керамики, и может приводить к значительному снижению емкости.