Пример краевой задачи для уравнения Гельмгольца в двумерном случае.

Смешанная краевая задача для уравнения Гельмгольца

Смешанная краевая задача для уравнения Гельмгольца имеет вид:

 

 

. Если - то имеем задачу Дирихле; если - задачу Неймана.

Дискретизация области представлена на рис.2.

При дискретизации задачи аппроксимацию граничных условий можно записать как порядка , так и .

Запишем аппроксимацию граничных условий порядка :

 

- здесь погрешность аппроксимации .

Теперь запишем аппроксимацию порядка , предполагая, что дискретизация области проведена так, как показано на рис.1:

 

,

 

 

- аппроксимация порядка .

Матрица здесь будет также трёхдиагональной.

 

Рассмотрим основные краевые задачи для уравнения Гельмгольца в двумерном случае. Начнем с задачи Дирихле (рис.3).

 

где - фактически функция одной переменной, т.к. на и связаны между собой.

- ограниченная область, - кусочно-гладкая кривая – граница области, - входные данные.

1) Дискретизация области.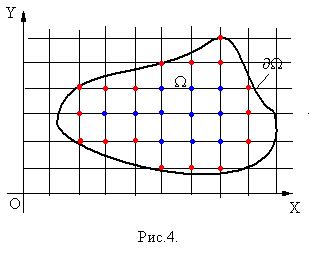

Будем строить двумерную сетку. Проводим систему прямых, параллельных и на одинаковом расстоянии друг от друга.

Точки пересечения этих линий – узлы сетки. Каждому узлу ставятся в соответствие координаты , т.е. ему соответствуют индексы . Некоторые узлы оказались внутри области, некоторые – вне области, некоторые на границе. Обозначим .

Построим дискретную область (рис.4). Для каждого узла определим соседей . Такое определение соседей связано с уравнением. Узел считается принадлежащим дискретной области, если сам он и все его соседи . Отметим узлы, принадлежащие синим цветом. Построим . , если сам узел , то хотя бы один из его соседей (эти узлы красного цвета).

Возьмем для примера в виде прямоугольника (рис.5).

 

Здесь .

2) Дискретизация задачи.

В каждом узле области заменяем производные, входящие в (1), разностными отношениями по формулам числового дифференцирования. Обозначим , тогда после замены:

 

 

Такая аппроксимация содержит 5 точек. Теперь понятно, почему определялась именно так. В (3) столько уравнений, сколько точек в . В случае прямоугольника можно более конкретно записать: .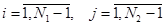

Все остальные этапы метода конечных разностей аналогичны одномерной задаче.