Алгоритм Евклида для целых чисел

Пусть a и b — целые числа, не равные одновременно нулю, и последовательность чисел

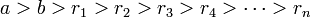
определена тем, что каждое r_k — это остаток от деления предыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть

a = bq₀ + r₁

b = r₁q₁ + r₂

r₁ = r₂q₂ + r₃

r_{k − 2} = r_{k − 1}q_{k − 1} + r_k

r_{n − 1} = r_nq_n

Тогда НОД(a,b), наибольший общий делитель a и b, равен r_n, последнему ненулевому члену этой последовательности.

Существование таких r₁,r₂,..., то есть возможность деления с остатком m на n для любого целого m и целого 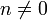, доказывается индукцией по m.

Корректность этого алгоритма вытекает из следующих двух утверждений:

§ Пусть a = bq + r, тогда НОД (a, b) = НОД (b, r).