Передаточные функции систем автоматического регулирования
Общие правила составления структурных схем.
1. Структурная схема обязательно должна иметь входные и выходные внешние связи (переменные), задаваемые из физических соображений.
2. Каждая входная переменная является независимой функцией и должна иметь только один вход в структурную схему.
3. Выходная переменная может замыкаться внутри структурной схемы и иметь выход в виде ответвления (система, замкнутая по выходной переменной) или не замыкаться внутри структурной схемы (система, разомкнутая по выходной переменной).
4. Все внутренние связи, определяемые системой уравнений, должны иметь входы и выходы.
Для построения структурных схем САУ используются два подхода:
- построение структурной схемы САУ по заданной системе дифференциальных уравнений;
- построение структурной схемы САУ по ее функциональной схеме, где каждый элемент системы описан дифференциальным или интегро-дифференциальным уравнением. Необходимо только отметить, что структуры функциональной и структурной схем совпадают. Отличие состоит в том, что на структурных схемах вместо уравнений элементов приводятся их передаточные функции, а вместо переменных их изображения по Лапласу.
Для упрощения структурных схем САУ используются специальные правила их преобразования, которые позволяют схему любой сложности свести к одному из трех типовых соединений звеньев (параллельному, последовательному и соединению с обратной связью).
Структурные схемы позволяют:
- дать ясное представление о процессах, происходящих в системе по сравнению с дифференциальными уравнениями;
- получать дифференциальные уравнения САУ по дифференциальным уравнениям отдельных элементов.
При наличии задающего и возмущающего воздействий схема одноконтурной САР приведена на рис. 2.3.
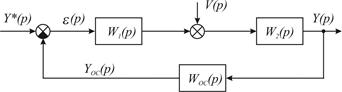
Рис. 2.3. Структурная схема одноконтурной САР
Для линейных САР при наличии нескольких входных воздействий на основе принципа суперпозиции находятся передаточные функции относительно каждого входного воздействия порознь. Затем они умножаются на изображения соответствующих воздействий и складываются.
Уравнение одномерной САР на рис. 2.3 имеет вид:
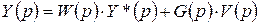 , (2.14)
, (2.14)
где W(p) – передаточная функция по задающему воздействию; G(p) – передаточная функция по возмущающему воздействию.
Передаточная функция W(p) определяется из условия, что v(t)=0. Тогда структурная схема САР на рис. 2.3 примет вид рис.2.4.
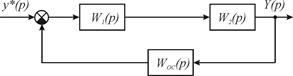
Рис. 2.4. Структурная схема одноконтурной САР по задающему воздействию
Отсюда имеем, что
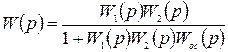 . (2.15)
. (2.15)
Передаточная функция G(p) определяется из условия, что y*(t)=0. Тогда структурная схема САР на рис. 2.3 примет вид на рис. 2.5.

Рис. 2.5. Структурная схема одноконтурной САР по возмущенному воздействию
Отсюда имеем, что
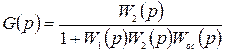 . (2.16)
. (2.16)
При исследовании точности САР часто рассматривается зависимость e(t) от задающего воздействия y*(t). Для характеристики этой зависимости вводится передаточная функция ошибки по задающему воздействию We(p), т.е. выходной переменной является изображение ошибки E(p).
Величина E(p) определяется на основе передаточной функции по задающему воздействию W(p), т.е.
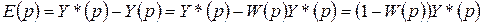 . (2.17)
. (2.17)
Отсюда имеем, что
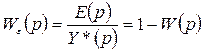 . (2.18)
. (2.18)
Если вместо W(p) подставить ее выражение (2.15), то
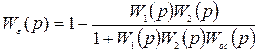
или после преобразования имеем, что
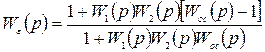 . (2.19)
. (2.19)
При единичной отрицательной обратной связи (Woc(p)=1)
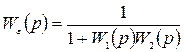 . (2.20)
. (2.20)
Так как W1(p)×W2(p)=Wp(p), где Wp(p) – передаточная функция разомкнутой части САР, то
 . (2.21)
. (2.21)
Структурная схема САР для определения We(p) приведена на рис. 2.6.

Рис. 2.6. Структура САР по ошибке