Преобразование Лапласа
Для анализа и синтеза САУ в ТАУ широкое распространение при решении дифференциальных уравнений получил операторный метод. Его основным достоинством является сведение решения системы дифференциальных уравнений к решению системы нормальных алгебраических уравнений.
В основе операторного метода лежит преобразование Лапласа:
 , (2.3)
, (2.3)
которое устанавливает соответствие между функцией действительной переменной t {x(t)} и функцией комплексной переменной p {Х(р)}, где 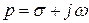 ; j – мнимая единица, т.е.
; j – мнимая единица, т.е. 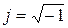 ; w - круговая частота. Функция времени x(t), входящая в интеграл Лапласа (2.3) называется оригиналом, а результат интегрирования – функция X(p) – изображением функции x(t) по Лапласу.
; w - круговая частота. Функция времени x(t), входящая в интеграл Лапласа (2.3) называется оригиналом, а результат интегрирования – функция X(p) – изображением функции x(t) по Лапласу.
Предполагается, что функция x(t), которая подвергается преобразованию Лапласа обладает следующими свойствами:
- x(t) определена и кусочно-дифференцируема на всей положительной числовой полуоси [0, +¥);
- x(t) =0 при t<0;
- существуют такие положительные числа M и с, что

при  .
.
Соотношение
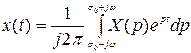 , (2.4)
, (2.4)
определяющее по известному изображению его оригинал (в точках непрерывности последнего) называется обратным преобразованием Лапласа, которое символически можно записать так:
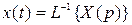 . (2.5)
. (2.5)