Статические и динамические характеристики систем автоматического управления

АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Для анализа и синтеза САУ необходимо иметь ее математическое описание, т.е. описание процессов, протекающих в системе на языке математики.

Математическое описание системы может быть задано:

- аналитически (в виде уравнений);

- графически (в виде структурных схем);

- таблично.

Уравнения, а также структурные схемы системы или ее элементов называются математическими моделями.

Для получения математической модели системы в ТАУ, в основном, используется поэлементный метод. Этот метод позволяет получать математическую модель системы путем объединения математических моделей ее отдельных элементов.

Математическую модель отдельных элементов обычно получают:

- на основе физических и других типов законов, которым подчиняются процессы, происходящие в элементах;

- экспериментально на основе функционального подхода с использованием принципа «черного ящика». При этом математическая модель должна как можно полнее отражать свойства оригинала и в тоже время быть по возможности более простой, чтобы не усложнять исследования.

При разработке математической модели системы или ее элементов учитывают два режима ее работы, приведенных на рис. 2.1.

Установившийся (статический) режим работы САР (участки I и III) – это режим, при котором характеристики системы не зависят от времени t.

Уравнения, описывающие поведение САР или ее элементов в установившемся режиме называются уравнениями статики, а их графики называются статическими характеристиками.Уравнения статики представляют собой системы нормальных алгебраических уравнений.

 

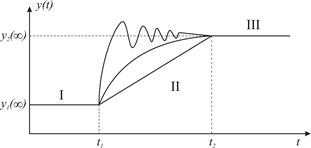
Рис. 2.1. Режимы работы САР

 

Переходный (динамический) режим работы САР (участок II) – это режим, при котором характеристики системы или ее элементов являются функциями времени.

Уравнения, описывающие поведение системы или ее элементов в переходном режиме называются уравнениями динамики, а их графики динамическими характеристиками.Уравнения динамики обычно представляют собой системы дифференциальных или интегро-дифференциальных уравнений.

Запишем уравнение динамики для одномерного элемента, приведенного на рис. 2.2. в следующем виде:

 

 

 

Рис. 2.2. Схема одномерного элемента

 

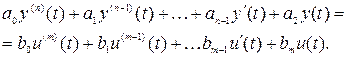(2.1)

Зачастую уравнение (2.1) делится на коэффициент а₀, чтобы коэффициент при старшей производной выходной переменной равнялся 1.

В ТАУ часто используется другая форма записи дифференциального уравнения

(2.2)

где k – коэффициент передачи элемента (системы); Т – постоянные времени, характеризующие инерционные свойства элемента (системы).

Уравнение (2.1) без правой части называется однородным дифференциальным уравнением, а с правой частью неоднородным дифференциальным уравнением.

Уравнения статики получаются из уравнений динамики при t®¥.

Математическая модель элемента (или части сложного элемента), которая отображает лишь его динамические свойства, а не физическую сущность происходящих в нем процессов, называется динамическим звеном.