Геометрическое распределение

Гипергеометрическое распределение

Определение 2.Случайная величина Х, принимающая целочисленные значения, имеет гипергеометрическое распределение, если 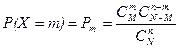, m = 0, 1, …, min(n, M). Можно показать, что .

 

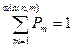Определение 3.Случайная величина X имеет геометрическое распределение, если

P(Х = m) = P_m= q^m-1p, m = 1, …

где q = 1–p, pÎ(0, 1). Геометрическое распределение имеет случайная величина X, равная числу испытаний по схеме Бернулли до первого наступления успеха с вероятностью успеха в единичном испытании р. Покажем, что Σp_i = 1

.
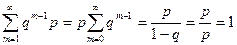