ЛЕКЦИЯ 3. АКСИОМАТИЧЕСКОЕ ПОСТРОЕНИЕ ТЕОРИИ ВЕРОЯТНОСТЕЙ. АКСИОМАТИКА КОЛМОГОРОВА

Классическое определение вероятности является весьма ограниченным. Ограниченность проявляется хотя бы в том, что события рассматриваются равновозможные, дискретные, число которых конечно. Рассмотрим, например, стрельбу по мишени. Если нас интересует только сам факт попадания по мишени, то элементарными исходами служат ω₁=1 и ω₂ = 0. Если нас интересует попадание в различные области мишени, то элементарными событиями могут быть ω₁₀ = 10, ω₉ = 9,… ω₀ = 0. В обоих случаях вероятности элементарных событий не одинаковы. Если нас интересует, в какую конкретно точку мишени попал стрелок, то произвольный элементарный исход ω = {X, Y} – представляет координаты точки попадания, а множество элементарных событий – это множество точек плоскости. Число точек плоскости не конечно и даже несчетно. Поэтому нужно так определить вероятность, чтобы это определение было одинаково пригодным для объектов различной природы.

При классическом определении вероятности в качестве события рассматривалось любое подмножество конечного множества элементарных событий W и вероятность события определялась как сумма вероятностей входящих в него элементарных событий. Если же W непрерывно, то имеет место континуум элементарных исходов. Попытка считать событием любое подмножество непрерывного множества W сопряжена с большими трудностями.

Поэтому в общем случае приходится иметь дело не со всеми подмножествами W, а лишь с определенным классом, замкнутым относительно операций объединения и пересечения.

Определение 1. Класс подмножеств из W, замкнутый относительно операций объединения, дополнения и пересечения, а также содержащий множества W, Æ, называется полем.

Будем обозначать поле буквой S. Минимальное поле состоит из полного и пустого множества S₀ = {W, Æ}. Другим примером поля событий служит класс из четырех событий S₁ = {W, Æ, А ,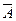}. Доказать самостоятельно.

Определение 2. Вероятностью называется числовая функция, определенная на поле событий S и обладающая следующими свойствами:

аксиома 1.Для любого события А Î S, Р(А) ³ 0;

аксиома 2. Вероятность достоверного события равна единице, P(Ω)=1;

аксиома 3. Вероятность объединения двух несовместных событий равна сумме вероятностей этих событий, т.е.

 

если АÎS, BÎS, А∩B = Æ, то P(АÈB) = P(А+B) = P(А) +P(B).

 

Во многих случаях выполнение аксиомы 3 требуется в расширенном варианте, а именно, аксиома 3 постулирует сложение вероятностей для конечного числа несовместных событий, в то время как в расширенном варианте речь идет о счетном числе несовместных событий –

аксиома 3'. Если А_i Î S, А_i ∩ А_j = Æ," i ≠ j , то.

 

Определение 3.Набор объектов {Ω,S,P} называется вероятностным пространством, где Ω – множество всех элементарных событий, S – поле, P – вероятность, определенная на поле S.

В лекции 2 формула условной вероятности (4) была выведена на основе классического определения вероятности, для общего случая эта формула является определением условной вероятности.

Определение 4. Условная вероятность наступления события А при условии В равна

P(a/b) = Р(АÇВ)/Р(В) = Р(АВ)/Р(В).

 

Определение 5. Событие А не зависит от события В, если

Р(А/В) = Р(А).

 

Теорема 1.Независимость событий взаимна, т.е. если событие А не зависит от В, то и событие В не зависит от А.