Формула Шеннона для пропускной способности

Из формулы Найквиста видно, что при неизменных остальных параметрах удвоение ширины полосы удваивает скорость передачи данных. Рассмотрим теперь связь между скоростью передачи данных, шумом и уровнем ошибок. Наличие шума может привести к повреждению одного или нескольких битов. При увеличении скорости передачи данных биты становятся "короче", поэтому при данном шуме поражается уже большее количество битов. Следовательно, чем выше скорость передачи данных при определенном уровне шума, тем выше уровень ошибок.

Пример воздействия шума на цифровой сигнал показан на рис. 4. Здесь шум складывается из фоновых помех относительно умеренного уровня и случайных всплесков импульсных помех. Цифровую информацию можно восстановить из сигнала путем дискретизации полученной формы сигнала, т.е. ее измерения через определенные промежутки времени. Как легко увидеть, случайного шума достаточно для изменения 1 на 0 или 0 на 1.

Рис. 4. Воздействие шума на цифровой сигнал

Все упомянутые выше понятия можно явно связать формулой, выведенной Математиком Клодом Шенноном[3] (Claude Shannon).

Как мы только что показали, чем выше скорость передачи данных, тем больший ущерб может нанести нежелательный шум. При данном уровне шума следует ожидать, что сигнал большей энергии имеет больше шансов прибыть по назначению неповрежденным. Ключевым параметром, присутствующим в этих рассуждениях, является отношение сигнал/шум (signal-to-noise ratio — SNR или S/N). Оно представляет собой отношение мощности сигнала к мощности шума, присутствующего в определенный момент передачи. Как правило, данное отношение измеряется в приемнике, поскольку именно в этой точке предпринимается попытка обработать сигнал и устранить нежелательный шум. Для удобства это отношение часто представляется в децибелах:

(1)

Данная формула в децибелах выражает превышение уровня сигнала над уровнем шума. Большое значение этого отношения свидетельствует о высоком качестве сигнала и, следовательно, необходимости введения меньшего числа промежуточных ретрансляторов.

Отношение сигнал/шум довольно важно при передаче цифровых данных, поскольку оно задает верхнюю границу возможной скорости передачи. Для максимальной пропускной способности канала Шенноном был получен следующий результат:

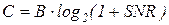, (2)

где C — пропускная способность канала в битах в секунду, а B — ширина полосы канала в герцах.

Сама формула Шеннона дает теоретически достижимый максимум. На практике, однако, достигаются значительно меньшие скорости передачи данных. Одной из причин этого является то, что в формуле учитывается только белый шум (т.е. тепловой) и не учитываются импульсные помехи, амплитудные искажения или искажения, вызванные запаздыванием.

Пропускная способность, выведенная в предыдущей формуле, называется безошибочной. Шеннон доказал, что если действительная скорость передачи данных по каналу меньше безошибочной пропускной способности, то при использовании соответствующих сигнальных кодов теоретически можно добиться безошибочной передачи данных по каналу. К сожалению, теорема Шеннона не дает способа нахождения таких кодов, но она дает критерий измерения производительности реальных схем связи.

Приведем несколько поучительных наблюдений, касающихся данной формулы. Кажется, что при фиксированном уровне шума скорость передачи данных можно увеличить за счет увеличения ширины полосы или интенсивности сигнала. Стоит отметить, впрочем, что при увеличении интенсивности сигнала в системе возникают нелинейные эффекты, приводящие к увеличению интермодуляционных помех. Кроме того, поскольку шум считается белым, то более широкая полоса предполагает введение в систему большего шума. Поэтому при увеличении ширины полосы В отношение сигнал/шум уменьшается, а не увеличивается.