Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона
Если закон распределения неизвестен, но есть основания предположить, что он имеет определенный вид (назовем его А), то проверяют нулевую гипотезу: генеральная совокупность распределена по закону А. Проверка гипотезы о предполагаемом законе неизвестного распределения производится при помощи специально подобранной случайной величины — критерия согласия.
Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения. Имеется несколько критериев согласия: «хи квад- квадрат» (критерий Пирсона), Колмогорова, Смирнова и др. Ограничимся описанием применения критерия Пирсона к проверке гипотезы о нормальном распределении генеральной совокупности (критерий аналогично применяется и для других распределений, в этом состоит его достоинство). С этой целью будем сравнивать эмпирические (наблюдаемые) и теоретические (вычисленные в предположении нормального распределения) частоты.
Критерий Пирсона не доказывает справедливость гипотезы, а лишь устанавливает на принятом уровне значимости ее согласие или несогласие с данными наблюдений.
Итак, пусть по выборке объема n получено эмпирическое распределение:
варианты 
частоты 
Теоретическими называются частоты, вычисленные по формуле
Допустим, что в предположении нормального распределения генеральной совокупности вычислены теоретические частоты. При уровне значимости 
требуется проверить нулевую гипотезу: генеральная совокупность распределена нормально. В качестве критерия проверки нулевой гипотезы примем случайную величину
Эта величина случайная, так как в различных опытах она принимает различные, заранее не известные значения. Ясно, что чем меньше различаются эмпирические и теоретические частоты, тем меньше величина данного критерия, и, следовательно, он в известной степени характеризует близость эмпирического и теоретического распределений.
Доказано, что при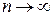 
закон распределения случайной величины 
независимо от того, какому закону распределения подчинена генеральная совокупность, стремится к закону распределения с k степенями свободы.
Число степеней свободы находят по равенству
В частности, если предполагаемое распределение нормальное, то оценивают два параметра (математическое ожидание и среднее квадратическое отклонение), поэтому r = и число степеней свободы
Если, например, предполагают, что генеральная совокупность распределена по закону Пуассона, то оценивают один параметр 
, поэтому r = 1 и k=s - 2.
Правило. Для того чтобы при заданном уровне значимости проверить нулевую гипотезу H0: генеральная совокупность распределена нормально, надо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия
и по таблице критических точек распределения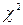 
по заданному уровню значимости и числу степеней свободы k = s-3 найти критическую точку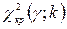 
.
Если нет оснований отвергнуть нулевую гипотезу.
Если нулевую гипотезу отвергают.
Замечание 1. Объем выборки должен быть достаточно велик, во всяком случае, не менее 50. Каждая группа должна содержать не менее 5-8 вариант; малочисленные группы следует объединять в одну, суммируя частоты.
Замечание 3. Для контроля вычислений формулу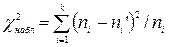 
преобразуют к виду
Пример: Известны
16; 13; 11; 15; 18; 19; 21; 18; 17; 15; 14; 16; 18; 17; 19; 15; 13; 12; 14; 16; 17; 20; 17; 17; 20; 19; 18; 22; 24; 18; 15; 14; 10; 12; 16; 18; 18; 19; 21; 23; 20; 22; 24; 17; 16; 14; 15; 18; 15; 11; 16; 17; 15; 13; 16; 17; 18; 14; 15; 19; 17; 18; 16; 13; 15; 17; 21; 23; 26; 19; 22; 24; 25; 20; 21; 24; 19; 23; 22; 20; 25; 21; 20; 22; 26; 19; 22; 23; 25; 28; 20; 21; 27; 19;10;26;12;28;11;27 - результаты независимых наблюдений над случайной величиной Х.
1. Сгруппировать эти данные в интервальную таблицу, подобрав длину интервала.
2. Построить гистограмму, полигон частот и эмпирическую функцию распределения.
3. Найти несмещённые оценки для математического ожидания и дисперсии случайной величины Х. Указать моду М0.
4. По критерию χ2 (Пирсона) проверить гипотезу о том, что случайная величина Х имеет нормальный закон распределения.
5. Найти интервальные оценки математического ожидания и дисперсии случайной величины Х с уровнем доверия γ=0,9.