Критерий Коши существования предела функции.

Можно получить необходимое и достаточное условие того, что функция имеет предел при , не прибегая к самому значению предела, а в терминах лишь значений самой функции в окрестности величины .

7#. Пусть функция определена в некоторой окрестности величины , кроме, быть может, . Будем говорить, что функция при удовлетворяет условию Коши, если для любого числа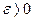существует такое числ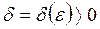о , что для любых 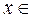, и ,.

(Критерий Коши). Для того, чтобы функция имела предел при , где - либо число , либо один из символов , , , +, -, необходимо и достаточно, чтобы она удовлетворяла условию Коши при .

(проводим всей группой в аудитории).