Свойства пределов функций.

! Отметим, что все функции, рассматриваемые в этом пункте, определены на некотором интервале 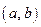, кроме, быть может, фиксированной точки .

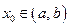1. Если и , то .

2. Если , то .

3. Если существует, то для любого числа справедливо равенство .

4. Если существуют и , то:

Ø =+;

Ø =;

Ø =, если .

! Отметим, что все эти свойства доказываются аналогично на основе как свойств пределов последовательностей, так и определения предела функции по Коши.

Сформулируем обобщенное определение предела функции, которым в дальнейшем и будем пользоваться в теории и практике математического анализа

6#. Величина (т.е. число или один из символов , +, -) называется пределом функции при (где - число или один из символов , , , +, -), если для любой - окрестности величины существует такая - окрестность величины , что для всех , .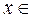

! Отметим, что введение такой терминологии позволяет упрощать доказательства теорем о пределах функции, проводя их единым образом, для двусторонних и односторонних, для конечных и бесконечных пределов функций независимо от того, стремится аргумент к конечному или бесконечному пределам.