Сформулируем второе определение предела функции (по Коши).
2#. Пусть функция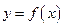 
определена на интервале 
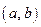, кроме, быть может, точки 
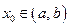. Число 
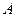называется пределом функции 
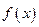в точке 
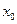, если для любого
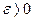существует такое число 
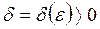, что для всех 
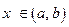, удовлетворяющих неравенству 
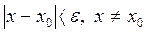выполняется неравенство 
.
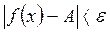** Рассмотрим графическую интерпретацию предела функции в точке (рис.1)
! Отметим, что оба определения (по Гейне и по Коши) представляют собой определение двустороннего предела функции в точке.
Сформулируем определение односторонних пределов – предела слева функции в точке и предела справа функции в точке.
3#. Пусть функция 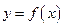определена на полуинтервале 
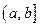(соответственно на 
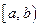). Число 
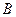называется пределом слева (справа ) функции 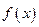в точке 
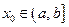(соответственно 
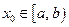), если для любого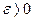существует такое числ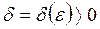о , что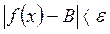
для всех 
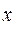, удовлетворяющих неравенству 
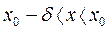( соответственно 
).
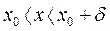! Обозначим: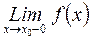 
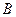= (соответственно 
= ).
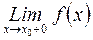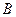! Отметим, что связь между односторонними пределами и двусторонним пределом устанавливает следующая теорема.