ЛОГИЧЕСКИЕ КОНСТАНТЫ И ПЕРЕМЕННЫЕ. ОПЕРАЦИИ БУЛЕВОЙ АЛГЕБРЫ

Для описания алгоритмов работы цифровых устройств необходим соответствующий математический аппарат. Такой аппарат для решения задач формальной логики в середине прошлого века разработал ирландский математик Д. Буль. По его имени математический аппарат и получил название булевой алгебры или алгебры логики.

Булева алгебра — это математическая система, оперирующая двумя понятиями: событие истинно и событие ложно. Естественно ассоциировать эти понятия с цифрами, используемыми в двоичной системе счисления. Далее будем их называть соответственно логическими единицей (лог. 1) и нулем (лог. 0).

Два элемента булевой алгебры, а именно событие истинно и событие ложно, называются ее константами. Будем понимать под ними значения соответственно лог. 1 и лог. 0.

Для того чтобы описать при помощи булевой алгебры поведение и структуру цифровой схемы, ее входным, выходным и внутренним узлам ставят в соответствие булевы переменные, которые могут принимать только два значения:

х = 0 , если х ¹ 1,

(2.4)

х = 1 , если x ¹ 0.

 

Определим множество операций, выполняемых над булевыми константами и переменными, а также постулаты, которым эти операции удовлетворяют. Основными

Табл. 1.2 Табл. 1.3

 

операциями булевой алгебры являются три операции: логическое сложение или дизъюнкцию (disjunction — разъединение, разобщение), умножение или конъ­юнкцию (conjunction — соединение, связь), отрицание или инверсию (inversion —перевертывание).

Логическое сложение.Эту операцию называют операцией ИЛИ или дизъюнкцией. Постулаты логического сложения двух переменных приведены в табл. 1.2.

Логическим сложением М независимых перемен­ных Х_m (m=0,...,M-1) называется операция, в результате которой получается логическая сумма в виде логической функции Y указанных независимых пере­менных, которая равна 1, если хотя бы одна из них Х_m (или x₀, или Х₁..., или Х_m) равна 1, и равна 0, если все Х_m равны 0.

Логическое сложение обозначается символа­ми "+", "v". Для записи логической суммы (функции) наиболее часто будем использо­вать первый символ. Для М = 2 логическая сумма записывается в виде: y=x₁+x₀. Запись чи­тается: "Х₁ или x₀", что на языке булевой ал­гебры означает: событие Y истинно (Y=1), если истинно (т.е. равно 1) хотя бы одно из со­бытий X₁ или x₀.

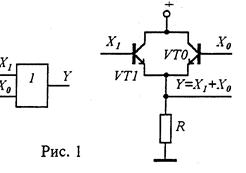
Элемент, с помощью которого реализуется логическое сложение, назы­вается логическим элементом (ЛЭ) ИЛИ. Графическое обозначение и пример реализации этого элемента для М = 2 приведены на рис. 1.

Следует отметить, что данная операция справедлива для произвольного числа переменных. Число переменных, над которыми выполняется операция, обозначается цифрой, стоящей перед ее обозначением. Так, для табл. 1.2 можно сказать, что она определяет операцию 2ИЛИ. Операция ИЛИ соответствует математической операции объединения множеств.

Логическое умножение.Эту операцию называют операцией И или конъюнкцией. Постулаты логического умножения двух переменных приведены в табл. 1.3.

Логическим умножением М независимых пере­менных Х_m (т=0,...,М-1) называется операция, в результате которой образу­ется логическое произведение в виде логической функции Y указанных неза­висимых переменных, которая равна 1, если все переменные Х_m (и x_0, и Х₁,..., и Х_M-1) равны 1, и равна 0, если хотя бы одна из переменных Х_m равна 0.

Операция логического умножения обозначается символами "•", "^", "&". Для записи логического произведения (функции) наиболее часто будем ис­пользовать первый символ и даже опускать его. Логическое произведение двух переменных (М=2) записывается в виде: y=x₁x₀. Запись читается: "x₁ и x₀", что на языке булевой алгебры означает: со­бытие Y истинно (Y=1), если истинно (т.е. рав но 1) и x₁ и x₀. .В табл. 1.8 приведено табличное представление логи­ческого произведения (функция Y₁) для этого случая.

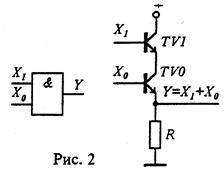
Элемент, с помощью которого реализуется логическое умножение, на­зывается ЛЭ И. Графическое обозначение и пример реализации этого эле­мента для М=2 приведены на рис. 2.

Следует отметить, что данная операция также справедлива для произвольного числа переменных. Она соответствует математической операции пересечения множеств. Число переменных, над которыми выполняется операция, также обозначается цифрой. В данном случае можно сказать, что табл. 1.3 определяет операцию 2И.

Отрицание.Операцию отрицания называют инверсией или дополнением. Для ее обозначения используют черту над соответствующим выражением. Операция определяется следующими постулатами:

если х = 1 , то х ≠ 0,

(1.5)

если х = 0, то x ≠ 1.

Логическим отрицанием независимой переменной Xназывается операция, в результате которой образуется функция Y, принимающая значение, противоположное значению X. В качестве Х

 

может фигурировать любая логическая функция.

 

Логическое отрицание записывается в виде функции Y=X, которая читается "не X" В табл. 1.8 приведены логические функции Y₁₀, Y₁₁ , полученные в результате выполнения операции логического от­рицания над функциями x₀ , Х₁, заданными набором из 4-х значений.

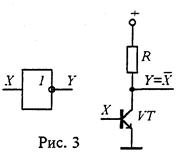
Элемент, с помощью которого реализуется логическое отрицание, называется ЛЭ НЕ. Его графическое обозначение и пример схемной реализации приведены на рис. 3.

Основные логические операции ИЛИ, И, НЕ позволяют аналитически описать, а ЛЭ ИЛИ, И, НЕ реализовать КУ любой степени сложности.