Энергия магнитного поля.

Магнитное поле, подобно электрическому, является носителем энергии. Естественно предположить, что энергия магнитного поля равна работе, которая затра­чивается током на создание этого поля.

Рассмотрим контур индуктивностью L, по которому течет ток I.

С данным кон­туром сцеплен магнитный поток Ф = L·I, причем при изменении тока на величину dI магнитный поток изменяется на dФ = L·dI.

Однако для изменения магнитного потока на величину dФ необходимо совершить работу dА = I·dФ= L·I·dI. Тогда работа по созданию магнитного потока Ф будет равна

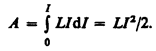
Следовательно, энергия магнитного поля, связанного с контуром, будет определяться соотношением

 

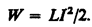
Для получения «объёмной» зависимости рассмотрим достаточно длинный соленоид.

Если соленоид находится в среде с магнитной проницаемостью – (m₀·m) – I=B·l/(m₀·m·N),а В=m₀mH , то

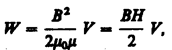
где V — объем соленоида.

 

Магнитное поле соленоида однородно и сосредоточено внутри него, поэтому энергия заключена в объеме соленоида и распределена в нем с постоянной объемной плотностью:

 

 

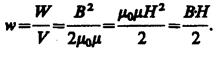
Примечание. Выражение для объемной плотности энергии магнитного поля имеет вид, аналогичный формуле для объемной плотности энергии электростатического поля, с той разницей, что электрические величины заменены в нем магнитными.