ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ПРОВОДНИК С ТОКОМ И ЗАРЯД
В качестве силовой характеристики магнитного поля в данной точке удобно использовать вектор , модуль которого , а направление совпадает с положительным направлением нормали к контуру. Эта величина называется вектором магнитной индукци.
.
Элементарный участок проводника длиной dl и током I создаёт в точке поля А индукцию dВi:
,
где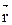 
радиус вектор, проведённый от элемента тока dl в току поля А; α угол которой образует радиус вектор 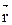с 
. Соотношение () носит название закона Био-Савара-Лапласа.
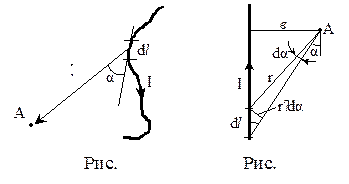В качестве примера получим формулу для расчета магнитного поля прямого тока. Все 
будут иметь одно направление, поэтому векторную сумму можно заменить сложением модулей. В точке А на удалении в от проводника:
; 
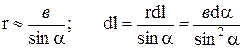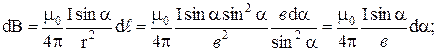
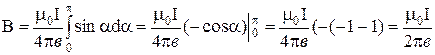
Для примера рассмотрим действие магнитного поля на контур с током. Предположим для простоты, что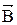 
лежит в плоскости перпендикулярной плоскости контура. Как видно из рисунка (вид сверху) возникает пара сил F1 = F2 = F, которая приложена к боковым сторонам контура и создает вращательный момент
М = F∙АС∙sinβ
Т.к. угол α между 
и 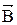равен 900 и ток прямолинейный, то сила, действующая на сторону длиной l в магнитном поле
F = I∙B∙l, тогда М = I∙B∙l∙АС∙sinβ = I∙S∙B∙sinβ = рм ∙В∙ sinβ; Мmax = рм ∙В
Величина, равная числу линий индукции пересекающих произвольно ориентированный плоский контур площадью S:
Ф = ВScosφ (1)
– называется потоком вектора магнитной индукции. [Ф] = Тл ∙м2 = Вб(вебер).
(тесла)
Т.к. 
характеризует силовое действие магнитного поля на ток, то индукция является аналогом напряженности электрического поля 
. Распределение вектора магнитной индукции в магнитном поле по аналогии с распределением в электрическом изображают с помощью силовых линий, касательные к которым в каждой точке поля совпадают с направлением . Силовые линии охватывают проводники с током и всегда замкнуты (рис.3 Тр,с177 прямой круговой). Их направление определяется правилом буравчика. Число линий на единицу площади поперечного сечения в данном месте соответствует модулю вектора .
Ампер установил, что на элементарный участок dl проводника с током I действует сила
, модуль которой dF = I∙B∙dl∙sinα, (1)
где α – угол между и 
. Направление этой силы определяется правилом левой руки: линии индукции входят в ладонь, четыре вытянутые пальцы направлены по току, тогда отставленный большой палец укажет направление силы. Отсюда следует, что сила Ампера всегда перпендикулярна плоскости, в которой лежат и .
Т.к. ток, это направленное движение зарядов, то на каждую движущуюся заряженную частицу в магнитном поле будет действовать сила. Рассмотрим участок проводника длиной l, поперечным сечением S и концентрацией заряженных частиц n. Плотность тока в проводнике – j = nqυ (υ – скорость дрейфа зарядов под возлействием электрического поля), а сила тока – I = j·S = nqυ·S, . Теперь силу, действующую на движущуюся заряженную частицу в магнитном поле – силу Лоренца, можно выразить соотношением:
, (2)
где N = n·Sl – общее число заряженных частиц на участке.
Направление силы Лоренца тоже определяется по правилу левой руки. Однако следует помнить, что для положительных зарядов четыре вытянутые пальца располагаются по вектору скорости, а для отрицательных – против.
Т.к. 
, то это означает, что сила Лоренца не может изменить величину скорости, но изменяет направление вектора скорости в пространстве, т.е. сообщает заряду нормальное (центростремительное) ускорение. В результате этого в простейшем случае, когда 
, заряд q в магнитном поле будет двигаться по дуге окружности, радиусом R:
→ 
(3)
и периодом обращения
. (4)
Эти простые соотношения лежат в основе объяснения принципов действия, таких известных приборов как ускорителей заряженных частиц и масс-спектрографа.
В общем случае, когда заряженные частицы влетают в магнитное поле под углом, то их движение можно представить как суперпозицию: равномерного прямолинейного со скоростью υïç = υ·cosa вдоль силовых линий; и равномерного обращения со скоростью υ^ = υ·sina вокруг силовых линий в плоскости перпендикулярной полю (рис. ). В результате образуется движение по спирали вдоль силовых линий. Винтовая линия (траектория) имеет радиусом R и шаг:
h = υïç∙Т = υТ ·cosa =
. (5)