Сложение взаимно перпендикулярных колебаний

Биения

Периодом колебаний, т. е. временем одного полного колебания; величина, обратная периоду называется частотой колебаний;

Амплитудой колебаний, т. е. величиной наибольшего отклонения от положения равновесия;

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

Квазиупругие силы. Условие возникновения
гармонических колебаний Дифференциальное уравнение
линейного гармонического осциллятора и его решение

 

Колебательным движением называют такое движение, которое характеризуется повторяемостью во времени значений физических величин, определяющих это движение или состояние. Колебания проявляются в различных физических явлениях. Ниже будем рассматривать колебания материальной точки.

Любое колебание характеризуется следующими параметрами:

3. Фазой колебаний, характеризующей состояние колебаний в любой момент времени;

4. Законом изменения колеблющейся величины со временем. Колебание, которое подчиняется закону синуса или косинуса, называется гармоническим

x = Acos(wt +α0), (7.5)

где х - смещение точки от положения равновесия в момент времени t; А - амплитуда колебаний; 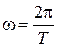- циклическая частота; Т - период колебаний; α0 - начальная фаза, wt + α0 - фаза колебаний в момент времени t.

Для возникновения механических колебаний необходимо выполнение определенных условий:

- наличие источника энергии, вызывающего смещение тела относительно положения равновесия,

- наличие возвращающей силы, направленной против движения, Fв .

- малые потери энергии на трение колеблющегося тела, т. е. диссипативные силы, которые являются непотенциальными (неконсервативными), должны быть достаточно малыми.

Возвращающая сила, которая пропорциональна отклонению точки от положения равновесия, называется квазиупругой:

Fв = –kx. (7.6)

Запишем дифференциальное уравнение колеблющейся точки с учетом (7.6):

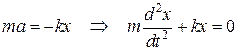. (7.7)

Обозначим 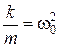, тогда получим уравнение:

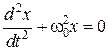, (7.8)

которое называется дифференциальным уравнением линейного осциллятора. Решением уравнения (7.8) является функция (7.1), описывающее гармонические колебания, которая представляет закон движения линейного осциллятора.

ω0 называется собственной частотой колебаний, которая зависит от упругой постоянной k и массы колеблющейся точки. Таким образом, гармонические колебания возникают под действием квазиупругой возвращающей силы.

Уравнение (7.4) носит универсальный характер и называется дифференциальным уравнением гармонических колебаний вдоль оси x. Коэффициент при x в данном уравнении равенквадрату собственной циклической частоты.

ПримерСкорость и ускорение при гармоническом колебательном движении.

Скорость и ускорение колеблющейся точки вдоль оси х определяются соотношениями:

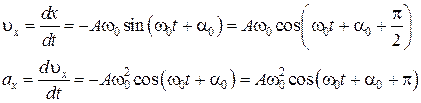(7.9)

также изменяются по гармоническому закону, при этом скорость и ускорение опережают смещение (7.1) по фазе соответственно на p/2 и на p.

 

Частоты собственных колебаний маятников
(математического, пружинного и физического)

 

При малых отклонениях от положения равновесия такие колебания имеют место в таких системах как пружинный маятник, математический маятник и физический маятник.

Пружинный маятник представляет собой невесомую пружину, к концу которой прикреплено тело массой m. При смещении шарика на величину х от положения равновесия на него будет действовать упругая сила

F = –kx.

Уравнение, описывающее колебания пружинного маятника, ничем не отличается от дифференциального уравнения (7.8) гармонического осциллятора. Частота собственных колебаний пружинного маятника равна:

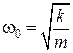. (7.10)

Период колебаний пружинного маятника равен:

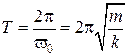. (7.11)

Математическим маятником называют материальную точку, подвешенную на невесомой нерастяжимой нити. При отклонении маятника на угол φ из положения равновесия (рис. 7.2) силу тяжести маятника 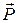можно разложить на две составляющие 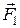и .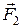

 

 
 

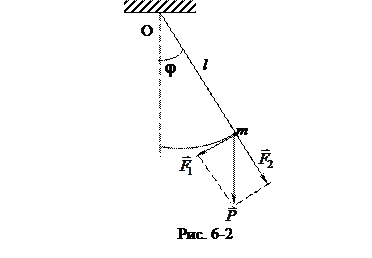Составляющая 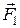стремится возвратить маятник в положение равновесия. На отклоненную точку действует момент силы M = –F1 l = –mgl sin φ. Согласно основному уравнению динамики вращательного движения Ie = M имеем:

.

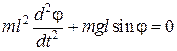Учитывая, что для малых a sin φ » φ, и разделив обе части последнего равенства на ml2, получим:

,

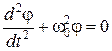где 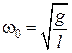– частота собственных колебаний математического маятника. Тогда период колебаний математического маятника не зависит от массы тела и равен:

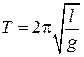. (7.12)

Если измерить период колебаний математического маятника, то можно определить и ускорение свободного падения g.

 
 

Физическим маятником называется любое твердое тело, колеблющееся под действием силы тяжести, которое не является математическим маятником, имеющее неподвижную горизонтальную ось вращения, не проходящую через его центр тяжести.

В этом случае на тело действует вращающий момент силы, равный M = –mgl0 sin φ. Согласно основному уравнению вращательного движения в проекции на горизонтальную ось вращения х, проходящую через точку О и перпендикулярную плоскости рисунка имеем

.

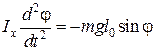Учитывая, что sin φ » φ для малых φ, и разделив обе части последнего равенства на Ix , получим:

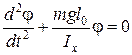. (7.13)

Из уравнения (7.9) следует, что частота собственных колебаний физического маятника равна:

.

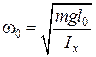Период собственных колебаний физического маятника равен:

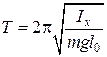. (7.14)

Сравнивая выражения для периода колебания физического маятника (7.10) с выражением для периода колебаний математического маятника (7.8) удобно ввести понятие приведенной длины физического маятника. Эта величина равна

.

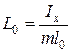Если отложить от точки О вдоль линии ОС расстояние, равное L0 , то получим точку О1 , которая лежит ниже точки С и называется центром качания маятника. Если перевернуть маятник и закрепить его так, чтобы центр качания О1 стал точкой подвеса, то приведенная длина для «перевернутого» маятника равна приведенной длине L0 и период колебания T1 = T2 . Такой «перевернутый» маятник называется оборотным маятником и используется для определения ускорения свободного падения.

 

7.3 Сложение колебаний одинакового направления методом
векторных диаграмм.

 

Суть этого метода векторной диаграммы. заключается в следующем. Из точки О на оси x откладывают вектор 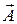, модуль которого A равен амплитуде колебаний, и направленный к оси х под углом, равным начальной фазе колебаний α0 (рис. 7.4). При вращении этого вектора с циклической частотой w0 его проекция на ось х в любой момент времени будет равна

x = Acos(w0 t + α0). (7.15)

Видно, что проекции вращающегося вектора на ось по форме совпадают с уравнением гармонических колебаний, если угловой скорости вектора сопоставить угловую частоту колебаний, а начальному углу - начальную фазу. Поэтому, сложение колебаний можно представить как сложение представляющих их векторов.

 

Рис.7.4

Рассмотрим сложение двух гармонических колебаний одинакового направления и одинаковой частоты.

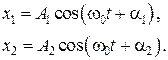(7.16)

Результирующее колебание представим в виде:

x = x1 + x2 = Acos(w0t + α).

Воспользуемся векторной диаграммой (рис. 7.5). На основании теоремы косинусов имеем:

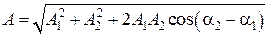, (7.17)

где A, A1 и A2 - модули векторов 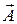,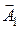и.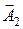

Из рисунка видно, что

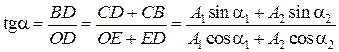. (7.18)

Из выражения (7.17) следует, что

если разность фаз α2 – α1 равна нулю, то амплитуда результирующего колебания равна сумме A1 и A2 ,

если разность фаз α2 – α1 равна p или –p (колебания совершаются в противофазе), то амплитуда результирующего колебания равна |A1 – A2 |.

 

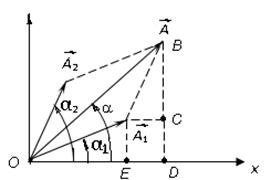
Рис.7.5

Рассмотрим сложение двух одинаково направленных колебаний, частоты которых мало отличаются друг от друга. Результирующее движение при этих условиях можно рассматривать как гармонические колебания с пульсирующей амплитудой. Такое колебание называется биением.Пусть частота одного колебания равна w1, второго w2 =w1 + Dw, при этом Dw << w. Уравнения:

x1 = Acos w1t, x2 = Acosw2t.

Складывая, получим

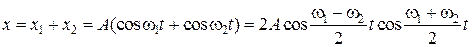. (7.19)

Выражение (7.19) показывает, что результирующее колебание также совершается вдоль оси x, а амплитуда результирующего колебания меняется со временем по закону 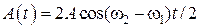(рис. 7.6).

 
 

 


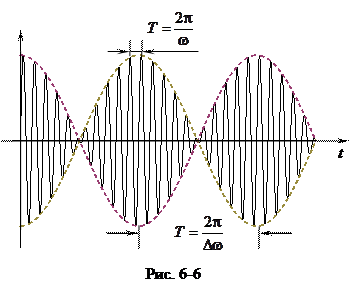Биения представляют собой колебания с усредненной частотой w=(w2 +w1)/2, а при каждом обращении амплитуды в ноль фаза биений скачком меняется на π.

 

Рассмотрим сложение гармонических колебаний совершающихся во взаимно перпендикулярных направлениях, в которых участвует материальная точка. Уравнения складываемых колебаний:

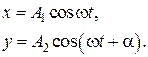(7.20)

Чтобы получить уравнение траектории, исключим из уравнений (7.20) время t. После математических преобразований получим уравнение:

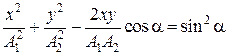. (7.21)

Выражение (7.21) - уравнение эллипса, оси которого ориентированы относительно координат х и у произвольно.

Рассмотрим некоторые частные случаи.

а) Разность фаз α равна нулю. В этом случае уравнение (7.17) принимает вид

,

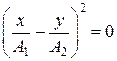откуда следует уравнение прямой

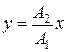. (7.18)

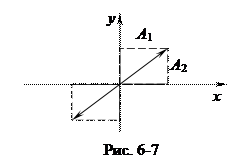
Результирующее движение точки является гармоническим колебанием вдоль прямой (7.18) с частотой w и амплитудой, равной 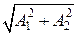(рис. 6-7).

 
 

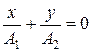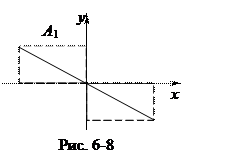
б) Разность фаз α = ±p. Уравнение (7.17) примет вид , откуда результирующее движение представляет собой гармоническое колебание вдоль прямой 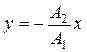(рис. 6-8).

 
 

в) При 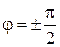уравнение (7.16) переходит в

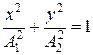, (7.19)

т. е. в уравнение эллипса, приведенного к координатным осям. При равенстве амплитуд A1 и A2 эллипс вырождается в окружность.

Если 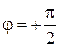, то движение совершается по часовой стрелке; при 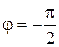движение происходит против часовой стрелки.

Если частоты двух складываемых колебаний не одинаковы, но кратны друг другу, то траектория имеет вид сложных кривых (фигуры Лиссажу).