Движение тел в жидкостях и газах

 

Рассмотрим тело, движущееся в жидкости вдоль прямой линии. Результирующая сила 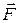, действующая на тело со стороны встречного по­тока жидкости, равна векторной сумме равнодействующих сил дав­ления,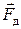, и сил трения, 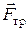, приложенных к поверхности тела:

.

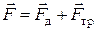Силу 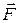можно разложить на две составляющие: силу лобовогосопротивления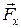, противоположную по направлению вектора скорости тела, и подъемную силу, направленную перпен­дикулярно этой скорости. Эти силы зависят от скорости потока, формы тела, его раз­меров, а также от свойств жидкости. Если жидкость идеальная, то, как пока­зывают расчеты, сила лобового сопротивления тела равна нулю, т.е. видеальной жидкости тело должно двигаться без всякого сопротивле­ния.

На рис. 5-5 показан вид линий тока идеальной жидкости, обтекающей длинный круговой цилиндр, ось которого расположена перпендикулярно к плоскости чертежа. Скорость жидкости отлична от нуля во всех точках поверхности цилиндра, за исключением критических точек а и b, в которых она равна нулю. На участках ас и ad скорость жидкости возрастает, а статическое давление убывает в соответствии с уравнением Бернулли. В точках с и d скорость максимальна, а давление минимально. На участках cb и dbскорость убывает, а давление возрастает. Линии тока симметричны относительно пло­скостей аb и cd. Поэтому ре­зультирующая всех элементар­ных сил давления жидкости на цилиндр равна нулю. Так как жид­кость идеальная, то нет и сил трения, т. е. 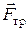= 0. Следо­вательно, результирующая си­ла, действующая на цилиндр, сила его лобового сопротивления и подъемная сила равны нулю.

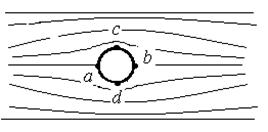
Рис. 5-5

Сила лобового сопротивления тела, обтекае­мого реальной жидкостью, всегда отлична от нуля. В вязкой жидкости возникает сила лобового сопротивления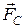, которая равна векторной сумме силы сопротивления трения и силы сопротивления давления. Сила сопротивления трения есть результирующая сил трения, дей­ствующих на все малые элементы поверхности тела. Сила сопротивления давления обус­ловлена тем, что из-за торможения жидкости, происходящего в погра­ничном слое, давление жидкости на лобовую часть поверхности тела не равно давлению на заднюю часть тела.

Сила лобового сопротивления, действующей на небольшой шарик, движущийся в вязкой жидкости с малой скоростью, определяется законом Стокса:

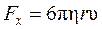, (6.15)

где η - коэффициент динамической вязкости жидкости, υ— скорость 'шара, а r - его радиус. Соотношение (6.14) справедливо при малых значениях числа Рейнольдса Re = ρυd/η < 1, где d = 2r – диаметр шара, ρ– плотность жидкости.

Если тело обтекается потоком жидкости или газа несимметрично, то возникает подъемная сила. Скорость потока около верхней части поверхности тела больше, чем около нижней (рис. 5-6). Соответственно, давление жидкости на ни­жнюю поверхность больше, чем на верхнюю. Поэтому результирую­щая сил давления на все малые элементы поверхности тела отлична от нуля.

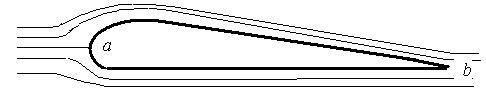
Рис.5-6

Соотношение между сопротивлением трения и сопротивлением давления зависит от формы тела и его расположения в потоке. У хо­рошо обтекаемого тела (например, крыла самолета, корпуса дирижабля, торпеды и т. п.) определяющую роль в лобовом сопротивлении играет сопротивление трения. Наоборот, лобовое сопротивление плохо обтекаемого тела в основном обусловлено сопротивлением давления. Это связано с тем, что при обтекании потоком вязкой жид­кости тел с большой кривизной поверхности (например, тел шарооб­разной формы) в хвостовой части тела возникает отрыв пограничного слоя от поверх­ности тела, приводящий к интенсивному вихреобразованию. В области, охваченной вихревым дви­жением жидкости, давление оказывается пониженным по сравнению с соответствующим участком лобовой поверхности. Поэтому возникает значительная равнодействующая сила, которая пропорциональна квадрату скорости движения тела.