Формула Пуазейля

Течение вязких жидкостей и газов в трубах.

 

При течении реальных жидкостей слои в этих жидкостях движутся с различными скоростями. Вблизи стенки канала (трубы), в котором течет жидкость, скорость течения намного меньше, чем вдали от нее. Из слоя газа с большой скоростью движения переносится импульс (ко­личество движения) к слою, движущемуся с меньшей скоростью. За счет передачи импульса от одного слоя к другому поперек движения скорость движения слоев уменьшается.

Рассмотрим течение жидкости вблизи плоской поверхности (рис.6.3). В направлении, перпендикулярном оси X, скорость движения во всех точках одинакова. Это значит, что скорость υявляется функцией только х. Как показывает опыт, импульс P, переносимый в единицу времени через единицу площади сечения, перпендику­лярного оси X, определяется уравнением

 

 

 

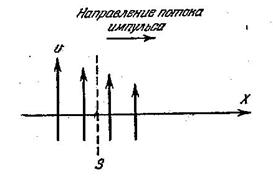
Рис.6.3

 

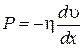, (6.10)

где 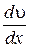- градиент скорости вдоль оси X,характеризующий быстроту изменения скорости вдоль этой оси (изменение скорости на каждую единицу длины). Знак минус означает, что импульс переносится в направлении уменьшения скорости. Коэффициент h - коэффициент динамической вязкости, который зависит от свойств газа или жидкости.

Вязкость проявляется в том, что любой слой газа или жидкости, движущийся относительно соседнего, испытывает действие некоторой силы. Эта сила и представляет собой силу трения между слоями газа.Уравнение (6.10) следует поэтому записать в виде

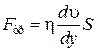, (6.11)

Выражение (6.11) - закон Ньютона для вязкого течения жидкости или газа.

Коэффициент динамической вязкости h согласно (6.11) численно равен силе трения между слоями площадью 1 м² при величине гра­диента скорости (в направлении, перпендикулярном к слоям), равном единице (1 м/сек на 1 м длины). Размерность h в СИ [h]= Па · с (паскаль-секунда).

В случае стационарного ламинарного течения жидкости по трубке небольшого радиуса R объем жидкости, протекший за секунду через сечение трубки прямо пропорционален разности давлений p₁ и p₂ у входа в трубку и на выходе из нее, четвертой степени радиуса R трубки и обратно пропорционален длине l трубки и коэффициенту вязкости h

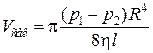, (6.12)

где V_сек – секундный расход жидкости. Соотношение (6.12) представляет собой формулу Пуазейля. Формула Пуазейля используется для определения коэффициента динамической вязкости сред η путем измерения объема V вытекающей жидкости за некоторое время t при заданном перепаде давлений. Этот метод называется вискозиметрическим.

Пример 6.2.Вывод формулы Пуазейля с помощью закона Ньютона для вязкого трения

Выделим объем жидкости или газа в виде цилиндра длиной l и радиусом r. При стационарном течении с постоянной скоростью сумма всех сил, действующих на выделенный объем, равна нулю. На данный объем действуют сила вязкого трения F_тр, , которая уравновешивается силой F_д, возникающей из-за перепада давления на длине трубки (рис. 6.4).

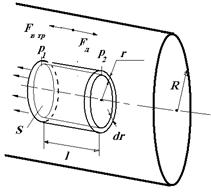
Рис.6.4

Сила F_тр, действует вдоль поверхности выделенного цилиндра с площадью S = 2plr и согласно закону Ньютона (6.11) равна

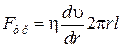. (6.13)

равна

.

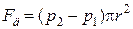Так как F_тр,по модулю равна силе F_д, то приравнивая два последних выражения, получим

Разделяя переменные и интегрируя это уравнение, получим распределение скорости течения в радиальном направлении:

.

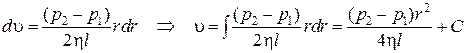Постоянную С определим из условия равенства нулю скорости на стенке трубы:

.

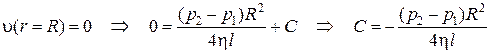С учетом последнего равенства:

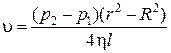. (6.14)

Объем жидкости dV, протекший за секунду через кольцевое сечение шириной dr (рис. 5-4), с учетом (6.14) равен:

.

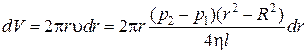Интегрирование последнего соотношения в пределах от 0 до R приводит к формуле (6.12).