Уравнение неразрывности
Поверхность, которая образована линиями тока, проведенными через все точки малого замкнутого контура, называют трубкой тока. Часть жидкости, ограниченную трубкой тока, называют струей.
Внешнее давление, производимое на жидкость или газ, передается ими во все стороны равномерно (закон Паскаля).
Режимы течений
Течение жидкостей и газов. Ламинарный и турбулентный
ГИДРОДИНАМИКА
Раздел физики, в котором рассматривают законы равновесия и движения жидких и газообразных сред, а также их взаимодействия с твердыми телами, называют гидроаэромеханикой.
Жидкие и газообразные тела не обладают упругостью формы – они легко принимают форму того сосуда, в котором находятся.
Наглядно течение жидкости изображается линиями тока, которые проводят так, что касательные к ним совпадают по направлению с векторами скоростей жидкости в соответствующих точках пространства.
В реальных жидкостях между отдельными слоями потока действует внутреннее (вязкое) трение. Причиной внутреннего трения является перенос молекулами импульса из одного слоя в другой.
Жидкость, в которой отсутствует внутреннее трение, называют идеальной жидкостью.
Наблюдается два вида течения жидкости (или газа) - ламинарное и турбулентное.
При ламинарном (слоистом) течении каждый выделенный слой скользит относительно соседних слоев, не перемешиваясь с ними. Ламинарное течение является стационарным и характеризуется постоянным во времени распределением поля скоростей по объему жидкости.
Турбулентное (вихревое)течение жидкости возникает когда вдоль потока происходит интенсивное вихреобразование и перемешивание жидкости. При этом режиме течения частицы жидкости приобретают составляющие скоростей, перпендикулярные течению.
Установлено, что характер течения зависит от значения числа Рейнольдса:
Re = rul/h, (6.1)
где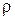 
- плотность жидкости (газа), 
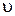- средняя по сечению трубы скорость жидкости, l - характерный размер канала (например, диаметр трубы), 
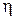- коэффициент динамической вязкости. Переход от ламинарного течения к турбулентному происходит при Re> Reкр. Например, значение критического числа Reкр для гладких цилиндрических труб составляет примерно 2300.
Рассмотрим трубку тока с сечениями dS1 и dS2 (рис.6.1) скорости жидкости в этих сечениях обозначим через υ1 и υ2, а плотность жидкости – соответственно ρ1 и ρ2.
Масса жидкости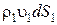 
, поступившей через сечение dS1 за единицу времени, будет равна массе жидкости
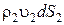, которая вытекла за единицу времени через сечение dS2.:
,
где dmсек – секундный массовый расход жидкости вдоль струи. Так как сечения были выбраны произвольно, то :
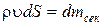. (6.2)
Соотношение (6.2) называется уравнением неразрывности.
Рис.6.1
В случае несжимаемой жидкости плотность одинакова во всех сечениях трубки тока и уравнение неразрывности имеет вид:
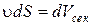
Если плотность жидкости и скоростьпостоянны по всему поперечному сечению S, то
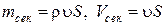. (6.3)