Уравнение Ван-дер-Ваальса. Изотермы газа Ван-дер-Ваальса и их сравнение с экспериментальными изотермами

Минимальная величина потенциальной энергии определяет существование вещества в том или ином агрегатном состоянии.

Если W_{n мин}< kT, где kT - удвоенная средняя энергия, приходящаяся на одну степень свободы хаотически теплового движения молекулы, то вещество находится в газоообразном состоянии.

Если W_{n мин} >kT - твердое состояние

Если W_{n мин} ~ kT - жидкое состояние.

 

Наличие сил притяжения и отталкивания приводит к тому, что при больших давлениях (когда расстояние между молекулами уменьшается) поведение реального газа будет отличаться от модели идеального газа. Силы отталкивания противодействуют проникновению данной частицы в ту область объема сосуда, которая занята другими молекулами. Собственный объем V₀, занятый частицей, можно представить представляется как объем шара с некоторым эффективным диаметром d. Поэтому «свободный объем» V*, в котором могут свободно (как в идеальном газе) двигаться молекулы реального газа, будет на некоторую величину меньше, чем объем V, занимаемый газом. «Свободный объем» будет равен

, (17.1)

где b — поправочный коэффициент для одного моля газа.

На расстоянии от стенки меньше некоторого эффективного радиуса межмолекулярного взаимодействия r_эфф на выделенную молекулу действует некоторая равнодействующая сила, направленная от стенки и стремящаяся уменьшить кинетическую энергию молекулыю

 

Рис.17.1

Величина работы этой силы зависит от количества молекул в сфере эффективного взаимодействия, т.е. от концентрации молекул в сосуде n. Поэтому можно утверждать, что работа сил притяжения пропорциональна концентрации молекул: А_пр = a₁n, и кинетическая энергия молекул при их подлете к стенке уменьшается на величину А_пр. Уменьшив среднюю кинетическую энергию молекул на А_пр в основном уравнении кинетической теории газов, получим выражение для давления газа на стенку сосуда:

. (17.2)

Учитывая, что и обозначая , получаем:

. (17.3)

Умножив обе части (17.3) на объем газа V* и положив nV* = νN_A, где N_A - число Авогадро, ν – количество молей газа, kN_A = R (R - газовая постоянная), получим выражение

. (17.4)

Величину p_i можно выразить через молярный объем V_μ, т.к. концентрация молекул .Тогда 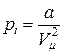, где - коэффициент пропорциональности, зависящий от природы молекул, или, учитывая, что , представим выражение для p_i в виде

. (17.5)

Подставив в (17.5) выражение (17.4) вместо р_i и (17.1) вместо V*, получим уравнение состояния Ван-дер-Ваальса для реального газа

. (17.6)

Следует отметить, что уравнение Ван-дер-Ваальса лучше согласуется с опытными данными, чем уравнение Клапейрона-Менделеева, особенно при высоких давлениях.