I. Построить интервальный вариационный ряд

Методические указания

Выполнения РАБОТЫ

Цель и последовательность

Произвести первичную обработку статистической выборки (n = 280) из непрерывной генеральной совокупности, построить статистическое распределение, эмпирическую функцию распределения, найти числовые характеристики выборки и по результатам обработки статистических данных выдвинуть гипотезу о законе распределения генеральной совокупности, оценить параметры предполагаемого распределения и провести статистическую проверку этой гипотезы.

.

Выполненную работу необходимо аккуратно оформить и сброшюровать.

Титульный лист должен быть оформлен по стандарту и содержать информацию о министерстве образования, названии кафедры, названии курсовой работы, номере варианта, фамилии студента и номере группы, фамилии руководителя, городе, годе.

Индивидуальное задание помещается сразу после титульного листа.

Рисунки могут быть выполнены в карандаше на обычной или миллиметровой бумаге.

Все страницы (рисунки, таблицы, формулы) должны иметь сквозную нумерацию арабскими цифрами.

Каждый раздел работы начинать с новой строки.

 

 

Варианты заданий разработаны сотрудниками кафедры прикладной математики ТГАСУ Л.Я. Пудан и А.В Ушаковым (задание к примеру, «Первичная обработка выборочных данных. Часть III») .

Варианты заданий выдаются преподавателем.

Дана выборка. Требуется:

Индивидуальное задание содержит n = 280 выборочных данных из непрерывной генеральной совокупности. Для составления интервального вариационного ряда необходимо разбить ее на 10 равных интервалов. Делается это следующим образом:

1. Найти среди выборки x_min и x_max. Записать размах выборки: Определить длину интервала h =, где k – число интервалов.

2. Записать 10 интервалов, считая каждый из них закрытым слева, а последний интервал закрыт и слева, и справа. Границы интервалов, следовательно, будут

3. Подсчитать для каждого интервала абсолютные частоты n_i (т. е. число выборочных данных, попадающих в каждый интервал), просматривая результаты наблюдений. При этом в интервал включают значения случайной величины, большие или равные нижней границе и меньшие верхней границы (в последний интервал включают и нижнюю, и верхнюю границы). Подсчет частот для каждого интервала удобно проводить методом «конвертиков». Суть этого метода состоит в том, что попадание значения случайной величины в тот или иной интервал отмечается точкой или черточкой. В результате каждому десятку будет соответствовать фигура, похожая на конверт:

 

 

Составить интервальный вариационный ряд абсолютных частот.

4. Найти центры каждого интервала:, где х_i – левый, а х_i+1 – правый конец интервала.

5. Вычислить для каждого интервала относительные частоты 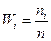. Составить вариационный ряд относительных частот.

6. В целях наглядности использовать графическое изображение вариационного ряда: гистограмму относительных частот и полигон относительных частот.

Чтобы построить гистограмму относительных частот, нужно на оси ОХ отложить все 10 интервалов и на каждом из них построить прямоугольники с высотой, равнойплотности относительных частот .

Чтобы построить полигон относительных частот, нужно на оси ОХ отложить центры интервалов и восстановить перпендикуляры, равные по длине плотности относительных частот. Концы соседних перпендикуляров соединяют отрезками.

II. Записать выборочную функцию распределения

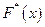и построить ее график

Выборочная функция распределения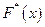имеет смысл накопительной относительной частоты. Составляется она с помощью вариационного ряда, т. е. суммы относительных частот, стоящих слева от х в вариационном ряду.

Графиком этой функции будет возрастающая ступенчатая линия, непрерывная слева. (На оси ОХ откладывают 10 интервалов и на каждом из них на высоте, равной значению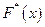, проводят отрезок прямой – ступеньку).

III. Найти числовые характеристики вариационного ряда

1.Найти выборочное среднее по всей выборке

, где х_j – все 280 данных значений.

2. Найти выборочное среднее значение по сгруппированным данным, т. е. с помощью вариационного ряда

.

3. Вычислить выборочную дисперсию по сгруппированным данным

и выборочное среднее квадратическое отклонение

( D_гр≈ D_В;σ_гр≈ σ_В ).

4. Найти относительную погрешность в вычислении выборочного среднего за счет замены выборки вариационным рядом

.